1. EPICSによる倒立振り子の制御

1.1. 始めに

EPICSでの制御の一例として、倒立振り子を制御するシステムを作成した。 状態制御則にもとづくフィードバックを実現するために、新たに EPICSレコードを作成した。

このレコードと、時間割込みを使うことで、VME計算機とリアルタイムOSを使ったシステムではkHz程度のフィードバックを実現することができた。 実際には、状態フィードバックを使うことで、 60Ｈｚ程度の処理間隔でも十分な制御性能を持つ。 この報告では、倒立振り子装置の概要、状態フィードバックの説明、状態フィードバック法によるフィードバックの設計、 EPICSレコードへの実装、実際の装置の性能と設計値との比較について述べる。

1.2. 倒立振り子装置

倒立振り子装置は、株式会社リンクスコーポレーション [A-2][A-3]が販売している倒立振り子装置を使用した。 装置は図 1.1に示した外観のように、倒立振り子が固定された台車と、それを一次元的に移動させるためのモータから構成されている。 また、台車の位置および、倒立振り子の傾きを検出するための検出装置〔ポテンシオ・メータ）が装着されている。 角度検出用のポテンシオ・メータは磁気抵抗素子を使ったもので、接触子を持たない、360度回転可能なタイプが使われている。 これらの検出器と、モータの制御入力はドライバ・ボックスに接続されている。 ドライバ・ボックスにはポテンシオ・メータのモニタの為の二つのアナログ出力とモータの速度指令値入力のためのアナログ入力端子が設けられている。

1.2.1. 制御装置

現行(2019年9月1日現在)の倒立振り子の制御システムは、

1. モータドライブ基盤を含む制御ボックス。
2. CPU/ADC/DAC/高速DIO モジュールを搭載したPLCシステム

から構成されている。[1]

PLCのCPUはLinuxベースのCPUを採用し、この上で直接EPICS[A-4]を動作させている。 EPICSデータベースからPLCの各種モジュールを利用するために必要となるデバイスサポートライブラリはこのPLC環境に標準のものを使っている。 また、倒立振り子の制御専用のレコードを開発し、制御アルゴリズムはこのレコードに実装した。

[1]	次の節にあるように当初はCAMACのIOモジュールとVME計算機を使って構築されていた。EPICSの上に構築されたアプリケーションは基本的に同じものが 使われている。

1.2.1.1. CAMACとVME計算機を用いた制御装置(Obsolete!) [2]

[2]	初代の制御システムはCAMACを使って構築された。今となっては歴史的資料としての意味しかないが、参考のために此処に残しておく。

此処で構築したシステムでは、標準的な EPICSの構成である VxWorksの動作する VMEシングルボード計算機 (Force PowerCore 6750など)を用いた 。 倒立振り子制御ボックスとのインターフェイスには CAMACの DAC/ADCボードを用いた。 VMEボード計算機に設置された CAMAC Serial Highway Driver経由で、 VME計算機上のフィードバックプログラムは台車位置および振り子の角度をよみとり、 また速度指令値をドライバ・ボックスに出力する。

VME計算機上には、 EPICＳのランタイム・データベースソフトウェアが稼働している。データベースには、CAMACからの入出力をつかさどるレコード、 CAMACから読みだされた値を物理的な量へ変換を行うレコード、フィードバックを構成するレコードなどがロードされている。

図. 1.1 倒立振り子装置とドライバ・ボックスの外観: 左)　稼働中の倒立振り子装置 右)倒立振り子のドライバ・ボックス

1.2.1.2. PLCを用いた制御装置

現行(2017年~)の倒立振子制御システムは、Yokogawa製のPLCを使って構築されている。 このシステムでは、PLCと言いながらもCPUとしてラダープログラムを実行するシーケンサではなく、 LINUXをOSとして使用するCPUを用いている。入出力はPLCのモジュールを使っている。 この上で、EPICS-IOCを構築し、EPICS-sequencerプログラムと組み合わせることで 倒立振子制御システムとしている。

振子の倒立状態を維持するためのフィードバックは,　旧システムと同じく、 EPIC recordとして実装されている (Feedback record)。

EPICS-sequencerは、台車可動域のチェック、倒立フィードバック停止後に台車を原点に移動させるFB, 振り上げ遷移の三つのstate setsを実装してある。

図. 1.2 PLCシステムの外観. DAC/ADC/高速入出力モジュールとLinuxが動作するCPUなどから構成されている。

1.3. 倒立振り子の物理モデルと制御

ここでは、制御対象である倒立振り子の物理的なモデルについて説明します。 この物理的モデルに基づいて線形化した制御モデルを作り、それに最適制御理論を 適用する事で、実際の制御システムが構築されています。

1.3.1. モデルの運動方程式から制御モデルへ

制御対象の物理モデルは質量 \(M\)の台車と質量 \(m\),慣性モーメント \(I\)の棒として表現される。棒の一端は台車の中央に固定されている。固定端から棒の重心までの距離を\(L\)とする。振り子が鉛直方向となす角度を \(\theta\)とした時、倒立位置\(（\theta=0)\)からのずれが小さいとするとその運動方程式 Eq.(1.1) および Eq.(1.2) は、

(1.1)\[\left(m + M\right)\ddot{z} − m l \ddot{\theta}= −\mu_z \dot{z}+ F_{ext}(t)\]

(1.2)\[\left(I + m l^2\right)\ddot{\theta} - m l \ddot{z} = +mgl\theta − \mu_\theta \dot{\theta}\]

である [付録 「第2.1章」参照]。此処で \(F_{ext}(t)\)は台車駆動装置から受ける外力である。 台車駆動装置は、速度指令値\(u(t)\)を受け取り、それが台車の速度\(\dot{z}\)となるような制御ループを持っている。 理想的な駆動装置では\(\dot{z}= u\)となるはずであるが、制御ループの時間遅れなどを考慮して（ [A-3][A-5]による）、

(1.3)\[ \ddot{z}= −\eta\dot{z} + \xi u\]

を採用することにする[3]。　\(\eta\)は時間遅れを表しており、平衡速度は\(\dot{z} = \frac{\xi}{\eta} u\)となる。 運動方程式は結局、

(1.4)\[\ddot{z} = −\eta\dot{z} + \xi u\]

および

(1.5)\[\left(I + m l^2 \right) \ddot{\theta} = m g l \theta - \mu_\theta\dot{\theta} + m l \left(-\eta \dot{z} + \xi u \right)\]

となる。これを行列形式で書き直すと、

(1.6)\[\begin{split}\frac{d}{dt} \begin{pmatrix} z \\ \theta \\ \dot{z} \\ \dot{\theta} \end{pmatrix} &= \begin{pmatrix} 0,& 0,& 1,& 0 \\ 0,& 0,& 0,& 1 \\ 0,& 0,& -\eta,& 0 \\ 0,& \frac{m g l}{\left(I + m l^2\right)},& \frac{- \eta m l }{\left( I + m l ^2\right)},& \frac{- \mu_\theta}{\left( I + m l ^2\right)} \end{pmatrix} \begin{pmatrix} z \\ \theta \\ \dot{z} \\ \dot{\theta} \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ \xi \\ \frac{ m l \xi}{\left(I + m l^2\right)} \end{pmatrix} u\end{split}\]

この装置では、台車の位置と、振り子の角度が観測量 \(y=\left(\begin{matrix}z, \theta\end{matrix}\right)\)である。行列形式では、

(1.7)\[\begin{split} y = \left(\begin{matrix}z, \theta\end{matrix}\right) = \begin{pmatrix} 1,0,0,0\\0,1,0,0 \end{pmatrix} \begin{pmatrix}z \\ \theta\\ \dot{z} \\ \dot{\theta} \end{pmatrix}\end{split}\]

となる。

[3]	結局まじめに取り扱おうとすると速度指定値 \(u\)と駆動装置のFBループ、台車からの反動を考慮したモータの回転の運動方程式までをふくんだ系を考えることになってしまう。 駆動用のモーターには、回転速度検出用のTG(Trubo Generator)が入っており、ドライボードはReference信号(速度指令値）とTGの信号の差分でフィードバックをかけているようなので、モーターの動作としては、\(\ddot{z}= \xi\left( u - \frac{\eta}{\xi}\dot{z}\right)\)で記述されると考えても良いだろう(?)。

1.4. フィードバックの設計

上記で得た制御対象のモデルに対して、現代制御理論に基づいてフィードバックを設計する。 フィードバックは状態推定器つき状態フィードバックにより構成する。この方法では、 状態推定器と状態フィードバックの二つのループのフィードバックパラメータを決定する必要があるが、 このパラメータは最適レギュレータの理論を用いて決定される。

1.4.1. 最適レギュレータ

フィードバックとしては、状態推定器付き最適レギュレータによる状態フィードバック法を用いる。状態フィードバック法は、制御対象の状態変数\(X\)と出力値 (観測値)\(Y\)が行列形式の線型な状態方程式、

(1.8)\[ \frac{d X}{d t} = A X + B u\]

(1.9)\[ Y = C X + D u\]

に従うとき、制御入力 (操作量)\(u\)を、

(1.10)\[ u= − K X\]

によって決定し、制御する方式である。この制御則の下では、制御対象の状態方程式は、

(1.11)\[ \frac{d X}{d t} = \left(A - B K \right) X\]

(1.12)\[ Y = \left( C - D K \right) X\]

となる。 \(A−BK\)の固有値の実部がすべて負であれば、明らかに、この系は \(t\rightarrow \infty\)で \(x\rightarrow 0\)である。行列 \(A, B\)が可制御の条件[4]をみたすなら、このような \(K\)が存在することが証明されている。倒立振り子の場合には、Freeな数値解析用プログラム Octave[付録「第2.3章」参照]を用いて、この系が可制御であることが次のようにして示される。

J=3.20e-4;
g=9.8;
m = 0.023000;
l = 0.20000;
mu =27.41e-6;
zeta=240;
xsi=90;
A=[0,0,1,0;0,0,0,1;0,0,-zeta,0;
   0,m*g*l/(J+m*l**2),-zeta*m*l/(J+m*l**2),-mu/(J+m*l**2)];
B=[0;0;xsi;xsi*m*l/(J+m*l**2)];
C=[1 0 0 0;010 0];
D=[ 0; 0 ];
rank(A)
rank(ctrb(A,B))

を実行すると、rank(ctrb(A,B))が状態空間の次元の4であることが示される。これは, この系が可制御であることを示している。

[4]	行列\(A\)および\(B\)について\(rank\left[B, AB, A^2B, \dots, A^{n-1}B\right] = rank(A)\)が成り立つ時、このシステムは可制御であると云われる。

\(A,B\)を安定化させるフィードバックゲイン \(K\)を求める方法は極配置法などの方法が知られているが、 ここでは最適レギュレータ法を用いてフィードバックゲイン \(K\)を求めてみる。最適レギュレータ法は、次の (目標）積分:

(1.13)\[ I = \int^{t_f}_{t_0} dt \left\lbrace x^T Q x + u^T R u\right\rbrace\]

が最小となるようにフィードバックゲイン \(K\)を求める方法である。 \(Q\)および \(R\)は正定値の対称行列で、目標積分の重みとなっている。 \(Q\)および \(R\)を選び直すことで、最終的なフィードバックループの振る舞いをコントロールする。 \(K\)は、代数的リカッチ方程式 (Riccati algebraic equation)、

(1.14)\[ P A + A^T P - P B R^{-1} B^T P + Q = 0\]

の正定対称解 \(P\)を用いて、

(1.15)\[ K = R^{-1} B^T P\]

と求めるられる。 Octaveでは (Matlabとおなじくlqr()関数を使うことで、フィードバックゲイン \(K\)を求めることができる。

R=1;
Q2=diag([50,1,1,1]);
[Kr2,p,e]=lqr(A,B,Q2,R);
eig(A-B*Kr2);

このプログラムの最後では閉ループの固有値を求めているが、この計算結果は、

ans =
-420.9663 + 0.0000i
-4.1659 + 2.3125i
-4.1659 -2.3125i
-2.4208 + 0.0000i

となって、すべての固有値の実部が負となっている。このことから、最適レギュレータ法による状態フィードバックは漸近安定であることがわかる。

1.4.2. 状態フィードバックの安定性

状態フィードバックの漸近安定性をつぎのように示すこともできる。次の量を考える。

(1.16)\[ I= x^T P x \geq 0\]

\(P\)は Ricatti方程式の正定対称解であるから、この量も正定値である。さらにこの量の時間微分をとると、

(1.17)\[\frac{d I}{d t} = x^T\left\lbrace P A + A^T P - P B K - K^T B P\right\rbrace x\]

(1.18)\[\begin{split}\frac{d I}{d t} &= - x^T\left\lbrace Q + P B R^{-1} B^T P\right\rbrace x \\ & = - x^T Q x - u^T R u < =\\\end{split}\]

となって、Q,Rが正定値の行列であることから、この量が \(t \rightarrow \infty\)で有界、したがって状態フィードバック系は安定であることが示された。

1.4.3. 状態推定器

状態フィードバックを行うためには各時刻での状態ベクトル \(x\)のすべての成分を知る必要がある。一般には、系の出力 \(y\)は状態ベクトル \(x\)をすべて再現出来るとは限らない。 しかしながら、系 \((A,C)\)が可観測[A-5]であれば 時系列データ \((u(0),y(0)), (u(1),y(1)), \dots (u(n),y(n))\)を用いて、時刻 \(n\)における状態べクトル \(x\)を推定することができる。このような状態推定器は、

(1.19)\[ \frac{d \hat{x}}{d t} = A \hat{x} + B u + H \left( y - C \hat{x} - D u\right)\]

として構成される。今、\(\hat{e} \equiv \hat{x} - x\) と定義すると、\(\hat{e}\)に関する運動方程式は、

(1.20)\[ \frac{d \hat{e}}{d t} = \left( A - H C \right) \hat{e}\]

となる。これから直ちに、 \(\left(A − H C\right)\)の固有値がすべて左半面にあれば、 \(t \rightarrow \infty\)で \(\hat{e} \rightarrow 0\)となることがわかる。 最適レギュレータの場合と同じように、系 \(\left(A, C\right)が可観測であれば、このような \ \)が存在することが保証される。 安定な状態推定器を与える状態推定器のゲイン \(H\)は、極配置法や、Kalman Filterによる方法で決められる。 カルマンフィルタでは、状態推定器のゲイン \(H\)は、再びリカッチ方程式、

(1.21)\[ A \bar{X} + \bar{X} A^T - \bar{X} C^T V^{-1} C \bar{X} +G W G^T =0\]

の正定対称解 \(\bar{X}\)を用いて

(1.22)\[ H= \bar{X} C^T V^{-1}\]

と求められる。上記のリカッチ方程式で、\(V\)および \(G W G^T\)は夫々出力値 (観測値)と入力値に含まれる雑音の共分散行列である。

それでは、雑音の無い系ではカルマンフィルタを用いることは出来ないのであろうか？いま、 \(V = \lambda \bar{V}, W= \lambda \bar{W}, \bar{X} = \lambda\bar{\bar{X}}\)とすると、\(\lambda\rightarrow 0\)の極限でも、カルマンフィルタのフィードバックゲインは有限な値で存在して、

(1.23)\[ H = \bar{\bar{X}} C^T \bar{V}^{-1}\]

となる。ただし、\(\bar{\bar{X}}\)は

(1.24)\[ A \bar{\bar{X}} + \bar{\bar{X}} A^{T} - \bar{\bar{X}} C^T \bar{V}^{-1} C \bar{\bar{X}} + G \bar{W} G^T = 0\]

の正定対称な解である。結局、\(\bar{V}, G\bar{W} G^T\)は、最適レギュレータの場合と同じ様に、最適化の重みを与えていると考えることが出来る。 Octaveではカルマンフィルターのゲインを、lqr関数を用いて求めることができる[5]。

G=eye(4);
sigw=eye(4);
sigv=eye(2);
[H,p,e]=lqr(transpose(A),transpose(C),G*sigw*transpose(G),sigv);
H=transpose(H)

\(eye()\)は単位行列を返す関数である。また、\(lqr\)の戻り値の \(p\)はリカッチ方程式の解、\(e\) は \(A − H C\)の固有値の配列である[6]。

[5]	Octave 2ではこのためにlqe関数が使えたが、SICOTベースの Octave3 ではlqe関数は提供されていない。->　GNU Octave 4.4.1で確認したところ、lqe()関数は利用可能でした。

[6]	可観測性は可制御性の双対であって、\((A^T, C^T)\)が可制御であることと等価である。

1.5. 状態推定器を用いたフィードバック

状態推定器をもちいて得られた状態ベクトル \(x\)をもちいて、最適レギュレータを構成することが出来る。このレギュレータの状態方程式は、

(1.25)\[ \frac{d x}{d t} = A x - B K \hat{x} + B u_i\]

(1.26)\[ \frac{d \hat{x}}{d t} = \left( A - B K - H C + H D K \right) \hat{x} + H y + B u_i\]

(1.27)\[ y = C x - D K \hat{x} + D u_i\]

(1.28)\[ u = -K \hat{x} + u_i\]

と書き表される。 \(x\)および \(x\)に関する状態方程式の部分を、行列形式で書くと、

(1.29)\[\begin{split} \frac{d}{d t}\begin{pmatrix} x \\ \hat{x}\end{pmatrix} = \begin{pmatrix} A,& -B K \\ H C,& A - B K - H C \end{pmatrix} \begin{pmatrix} x \\ \hat{x}\end{pmatrix} + \begin{pmatrix} B \\ B \end{pmatrix} u_i\end{split}\]

となる。この拡大系の係数行列の固有値は、 \(A − H C\)および \(A − B K\)の固有値を合わせたものになる。すなわち、フィードバック系と状態推定器を組み合わせたことによっては、新しい固有値は出てこない。これを分離定理とよぶ。

(1.30)\[\begin{split} &\det\left|\begin{matrix} A - \lambda ,& -B K \\ H C,& A - B K - H C-\lambda \end{matrix} \right| \\ =&\det\left|\begin{matrix} A - H C - \lambda ,& -A +HC +\lambda \\ H C, & A - B K - H C-\lambda \end{matrix} \right| \\ =&\det\left|\begin{matrix} A - H C - \lambda ,& 0 \\ H C, & A - B K -\lambda \end{matrix} \right| \\ =&\det\left|A - H C - \lambda \right| \det\left| A - B K -\lambda \right| \\\end{split}\]

先程導入した状態推定器の誤差 \(e\)を用いて、上記の状態方程式を書き直すと、

(1.31)\[\begin{split} \frac{d x}{d t} &= \left( A - B K\right) x - B K \hat{e} + B u_i \\ \frac{d \hat{e}}{d t} &= \left( A - H C \right) \hat{e}\end{split}\]

となることからも、分離定理が成り立つことがわかる。 \(\hat{e}\)の運動は \(A − H C\)の固有値できまり、 \(x\)の運動は \(A − B K\)の固有値できまる。さらに状態推定器の誤差 \(e\)は \(x\)の運動にたいして、外力として作用することがわかる。

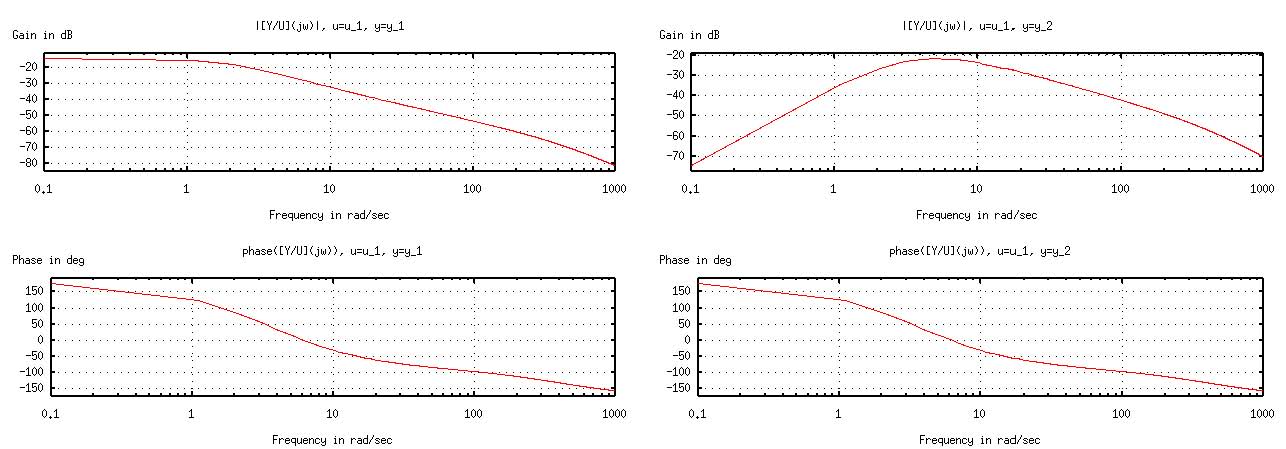
1.5.1. Bode線図

このようにして設計したフィードバックシステムの周波数応答を見るために、 bode線図を書いてみる。次の Octave program

AF=[[A -B*Kr];
[H*C, A-B*Kr-H*C]];
BF=[B;B];
CF=[C [0,0,0,0; 0,0,0,0]];
DF=[0;0];
sys=ss2sys(AF,BF,CF,DF)
bode(sys,[0.1:1000],1,1)
bode(sys,[0.1:1000],2,1)

によって閉ループ系の Bode線図を描いたものが、図. 1.3である。この系は 1入力 2出力系であるので、ここに示したように、二つの bode線図が書かれる。

図. 1.3 倒立振り子系の Bode線図。どちらも入力：台車速度に対する　 a) 出力：台車位置 , b) 出力：振り子角度のゲイン（上図）と位相（下図）の周波数依存性を示している。

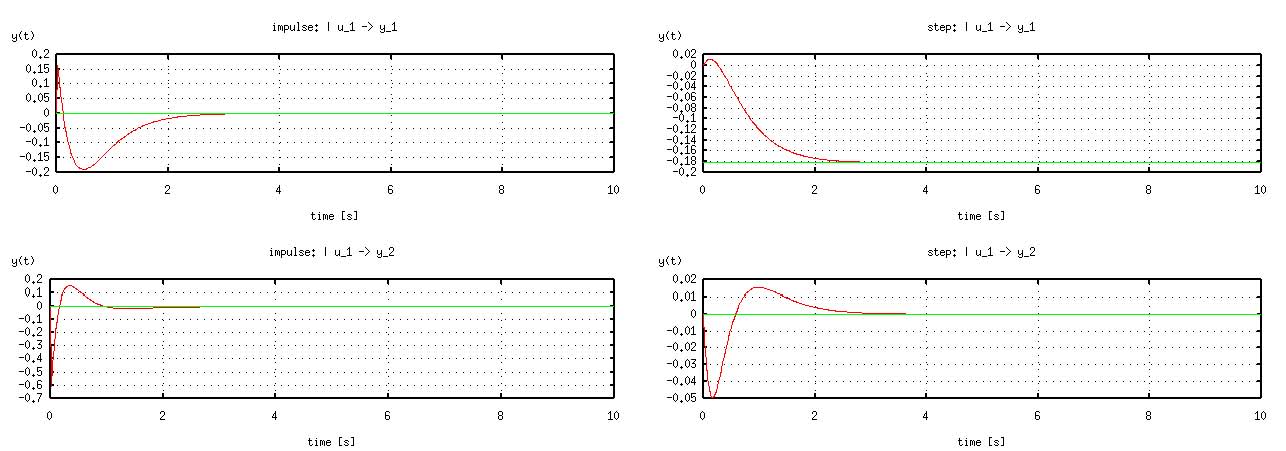
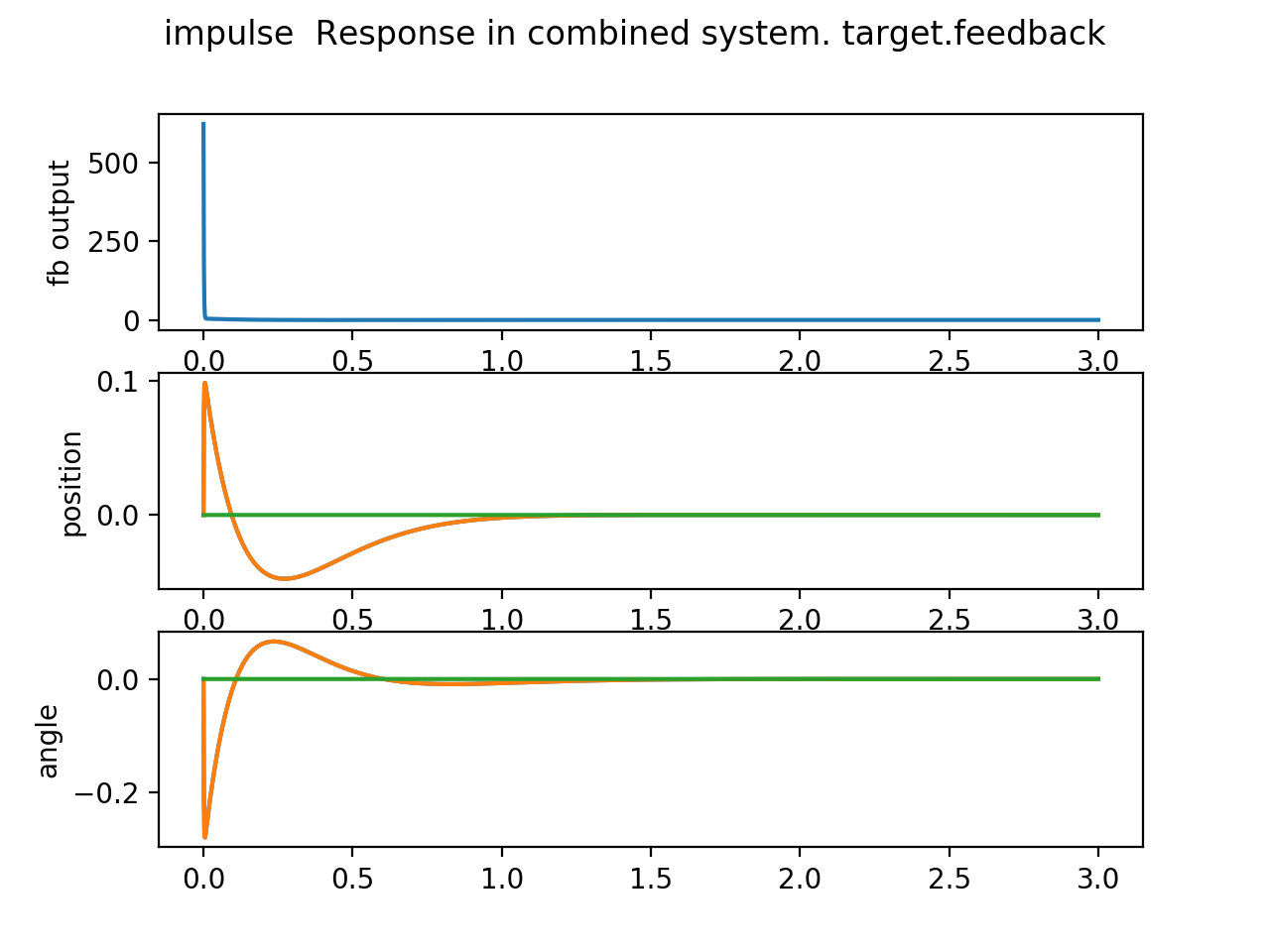
1.5.2. 制御システムのシミュレーション

次に閉ループ系の応答をみる。 Octaveにはインパルス入力とステップ入力に対する応答をプロットする関数、impluse()および step()が用意されている。

sys=ss2sys(AF,BF,CF,DF)
step(sys,1,10,400)
impluse(sys,1,10,400)

これによって描かれた系の応答が、図 1.4である。

図. 1.4 閉ループ系のインパルス入力 (a)およびステップ入力 )(b)による応答。上図：台車位置 (m)、下図：振り子の振れ角 (rad).横軸：時間（秒） a)インパルス入力応答。 b)ステップ入力応答。

1.5.3. 離散化

ここまでの解析は連続系の状態方程式としての解析であった。このフィードバック則を EPICSなどの計算機ベースの制御システムに実際に組み込むためには、時間方向に関しての離散化が必要である。ここでは、 Octaveの c2d()関数を用いて、離散化を行った。

sysd=c2d(ss2sys(A-B*Kr3-H*C,H,-Kr3),1./60);
Ad=sysd.a;
Bd=sysd.b;
Cd=sysd.c;
Dd=sysd.d;

\(Ad, Bd, Cd, Dd\)はゼロ次ホールド法によって離散化された系の状態方程式の係数行列である。 c2dの最後の引数は時間の離散化の単位時間 \(Ts\)である。ここでは 60Hzで制御を行うこととし 1/60.を指定した。

1.5.4. 測定誤差の影響

このフィードバック系で測定値に誤差があった場合の影響を考察する。測定誤差を \(\delta y\)とすると、観測値 \(y\)は、

(1.32)\[y = C x + D u + \delta y\]

となる。これから系の状態方程式は、

(1.33)\[\begin{split}\frac{d x}{d t} = \left(A - B K\right) x - B K \hat{e} \\\end{split}\]

(1.34)\[\frac{d \hat{e}}{d t} = \left(A - H C\right) \hat{e} + H \delta y\]

と変更される。形式的にこの方程式の解は、

(1.35)\[ \hat{e}(t) = \int^t_{-\infty} e^{\left(A - H C\right) \left(t - t'\right)} H \delta y d t'\]

(1.36)\[ x(t) = - \int^t_{-\infty} dt'' e^{\left(A - B K \right) \left(t - t''\right)} B K \int^t_{-\infty} e^{\left(A- H C\right)\left(t'' - t'\right)} H \delta y dt'\]

と書くことが出来る。今誤差が定数であるとすると、定常状態では、

(1.37)\[\begin{split}0 = \left(A - B K\right) x - B K \hat{e} \\\end{split}\]

(1.38)\[ 0 = \left(A - H C\right) \hat{e} + H \delta y\]

を解くことによって、定常状態の状態ベクトルを求めることが出来る。

(1.39)\[ x_{st} = \left( A - B K \right)^{-1} B K \hat{e}_{st}\]

(1.40)\[ \hat{e}_{st} = - \left( A - H C \right)^{-1} H \delta y\]

係数行列 \(A\)の性質によって[7], \(\left(A − B K\right)^{-1} B K\)は第一行を除いて総ての成分が 0となる。したがって、\(\delta y\)に係わらず、定常状態で残る誤差の影響は台車位置のずれだけになる[A-5]。

[7]	プログラムプログラム 1.1をSageMath[A-6]で実行することで、\(\left(A − B K\right)^{-1} B K\)は第一行だけがゼロ出ない成分を持つことが確認できる。

プログラム 1.1 Error propagation from y to state space.

for i in range(4):
  var('b_%d'%i)
  var('k_%d'%i)
  for j in range(4):
    var('a_%d%d'%(i,j))
A=matrix([
     [0, a_01, a_02, a_03],
     [0, a_11, a_12, a_13],
     [0, a_21, a_22, a_23],
     [0, a_31, a_32, a_33]]);
B=matrix([[b_0],[b_1],[b_2],[b_3]]);
K=matrix(((k_0, k_1, k_2, k_3)))
((A-B*K)**(-1)*B*K).simplify_full()

1.6. EPICSを用いた制御システムへの実装

以上に述べた制御則を EPICSにもとづく制御装置に組み込むために、専用のレコード InvPendRecordを作成した。 制御プログラムの本体部分は参考文献 [A-5][A-7][A-8][A-9]を参考にした。 制御プログラムなどに必要な係数は、 EPICSの SCANの繰り返し時間毎に InvPendRecordに定数として書き込まれている。 SCANフィールドを変更すると適切な係数が選ばれる。実機では、SCANの周波数を５ Hz以下にすると、系を安定化することが出来なかった。

InvPendRecordの process関数中では、取り込んだ台車の位置と、振り子の角度から、状態推定器を更新し、それにもとづいて新たな出力指令値を計算している。

連続系では、

(1.41)\[\begin{split} \dot{\hat{x}} &= \left( A - B K_r - H C \right) \hat{x} + H y \\ & = \left(A - B K_r - H C\right)\hat{x} + Hy + (B - H D) u_i\end{split}\]

(1.42)\[ u_c = - K_r \hat{x}\]

であるが、離散系では:

(1.43)\[ \hat{x}(k+1) = \hat{A}_d \hat{x}(k) + H_d y(k)\]

(1.44)\[ u_c(k+1) = -K C_d \hat{x}(k+1)\]

となる。 VxWorksを用いるVME計算機などで稼働するEPICSの periodic scanは VxWorksの Tickである 1/60秒以下にすることは出来ない。これ以上の繰り返しでレコードのプロセスを行うために、 VxWorks では Auxially Clock による時間割込みを利用することが出来る。この仕組みを利用することで、 60Hz～1KHzまでのフィードバックループによる倒立振り子の制御も可能である。

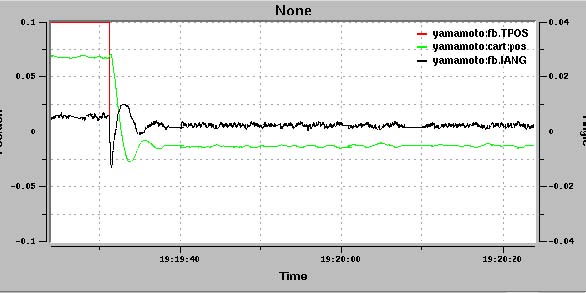
1.6.1. 倒立振り子装置の動作試験

実機での指令値のステップ変更に対する応答を次の図 (図-1.5)に示す。 離散化されたフィードバックの繰り返し周波数はこの場合、60Hzである。 倒立振り子を立てるだけならこの程度の繰り返しでも充分である[8]。 実測値と、シミュレーションによる結果は定性的にはよくあっている。

図. 1.5 実機のステップ入力に対する応答の実測値。赤：台車位置設定値、緑：台車位置の読み出し値、黒：振り子の振れ角 (rad)、横軸：時刻（全幅が一分）

[8]	振り上げなどの制御を行うためには、フィードバック制御の繰り返しは速い方が良いだろう。繰り返しの速度と共に繰り返し周期の精度も問題になる。VxWorksなどのリアルタイムOSでは繰り返し周期の精度が高い。

1.6.1.1. フィードバックの調整

ここで採用した状態フィードバックでも最適化条件のパラメータを調整することで、最終的な動作の調整を行う。 よく使われるPID制御の調整と比べてこの方法が有利なのは、パラメータを調整してもシステム全体の安定性は 保証されていることである。

フィードバックの調整は Eq.(1.13) のパラメータ \(Q\) および \(R\) を変更することで行う。 \(Q\) および \(R\) は任意の正定値の行列で良いが、実際的には対角行列が 使われることが多いでしょう。全体のスケールを変更しても、結果を変えないことから、独立なパラメータとしては、4+1-1 = 4 のパラメータがあることになります。

台車の位置がレールの範囲の中に収まっていること、振り子が倒立状態を保つこと、モータ駆動電圧が10Vを超えないことを考えて、最終的に(2019.9.26現在)次のパラメータ を採用しています。

(1.45)\[\begin{split}Q &= diag([1./0.05**2, 1/0.2**2., 1., 1.])\\ R &= 1./3.**2*diag([1])\end{split}\]

このパラメータを採用した時のシステムのステップ応答は次の図(図. 1.6)のようになります。

図. 1.6 システムのステップ応答。最上段のグラフはフィードバックの出力、二段目は台車の位置、三段目は振り子の角度を示している。この図の作成はpytho controlモジュールの step_response関数を用いて行っています。

1.6.1.2. 離散化アルゴリズムの選択

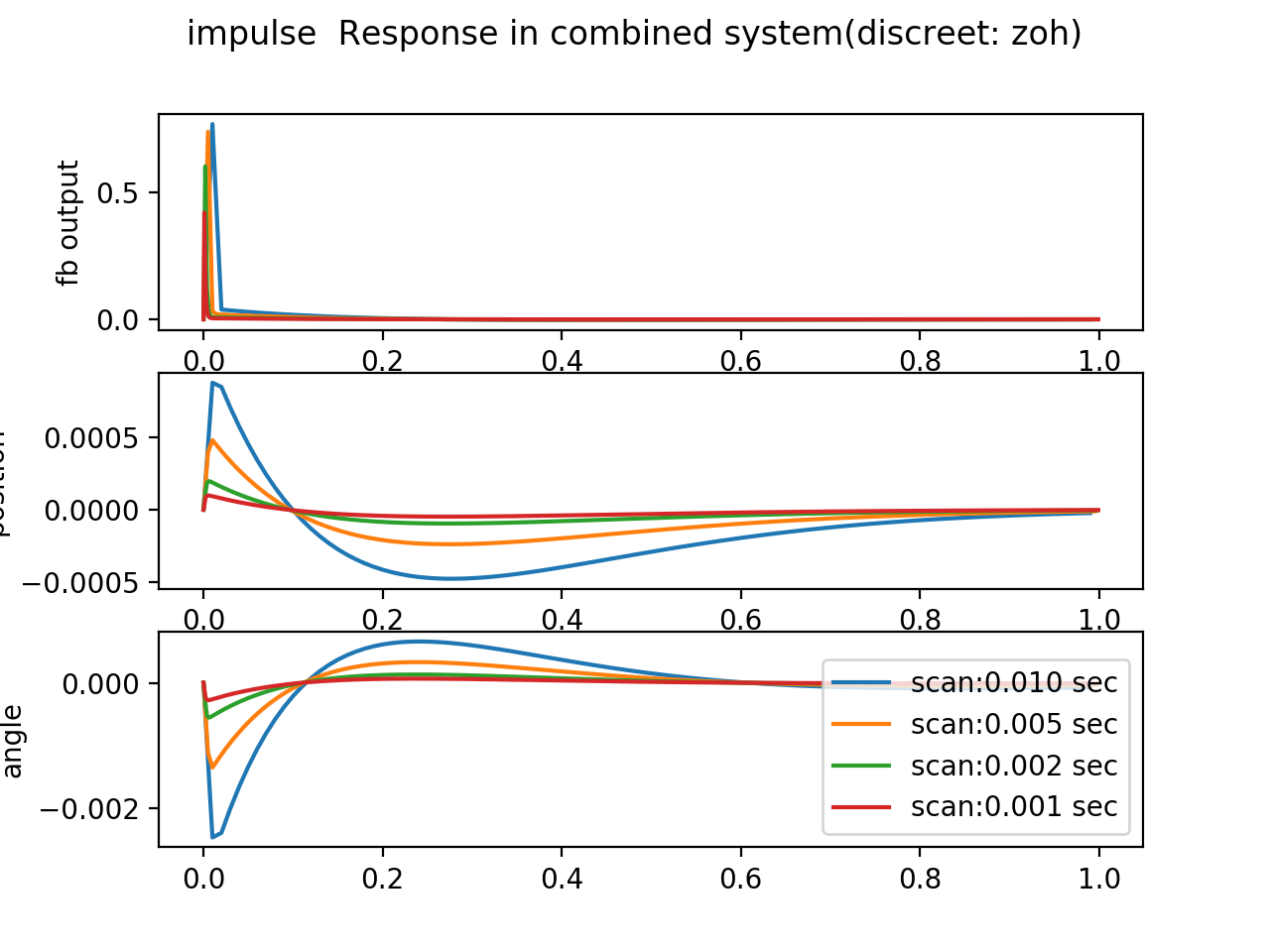
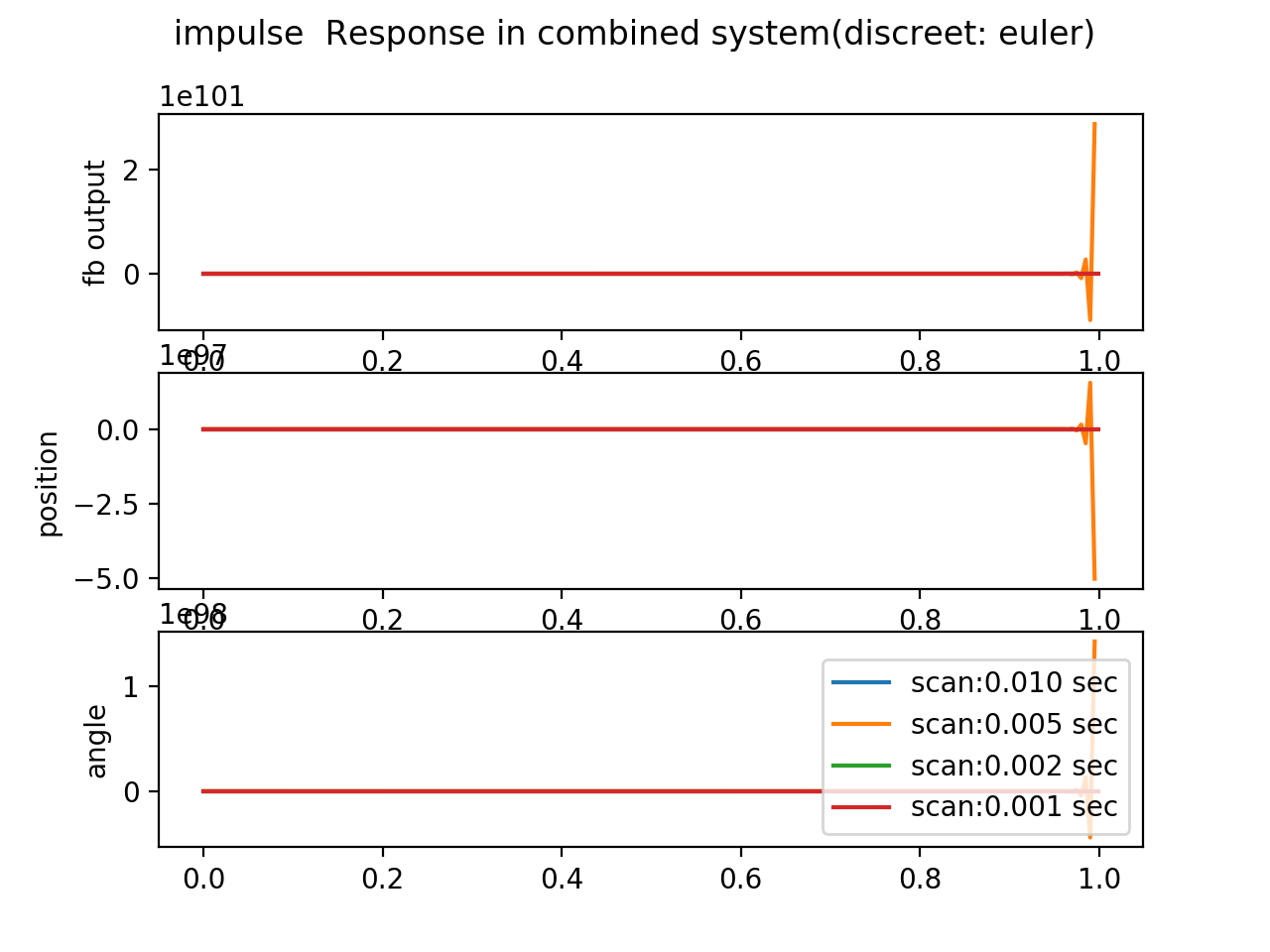
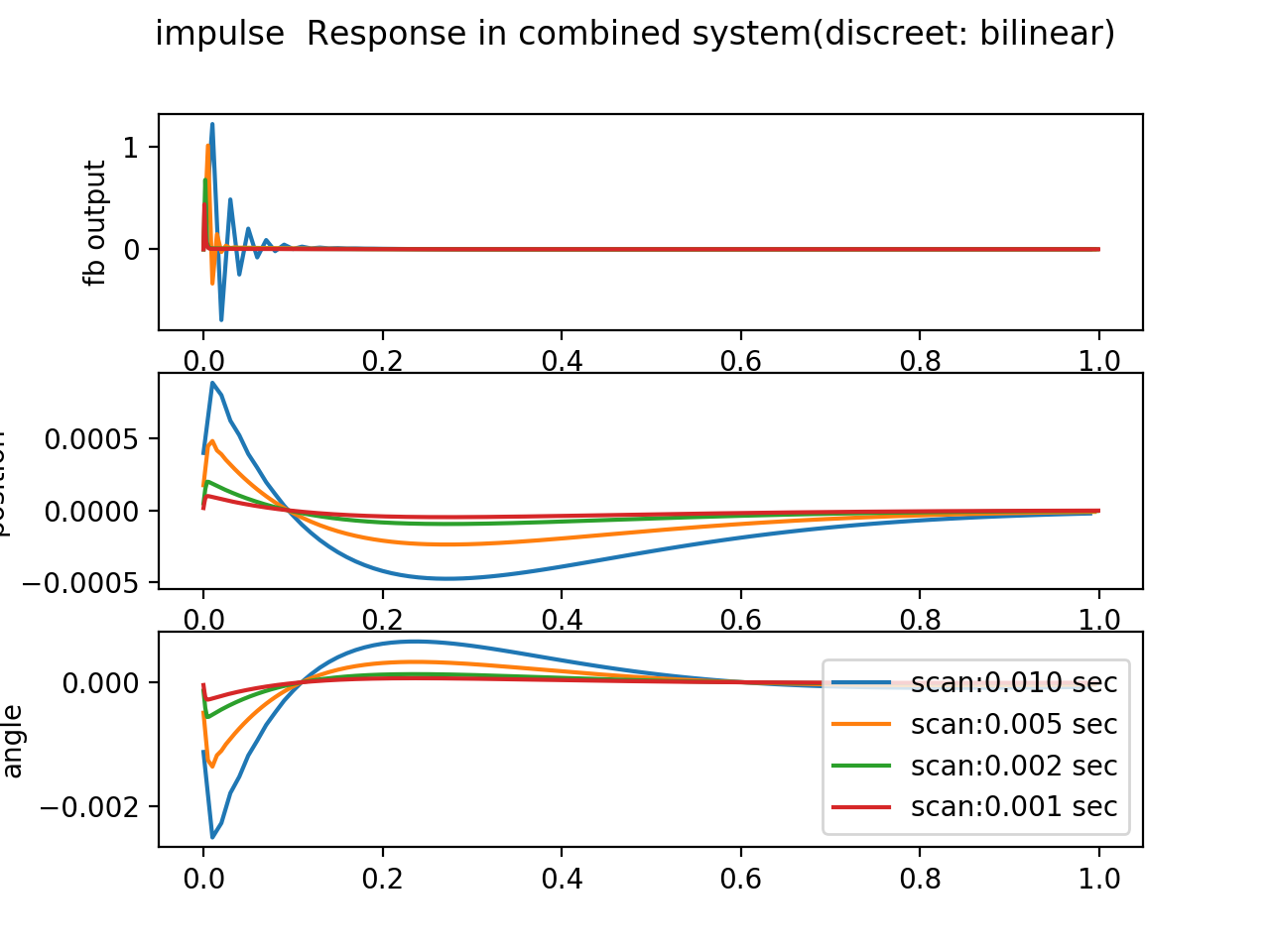
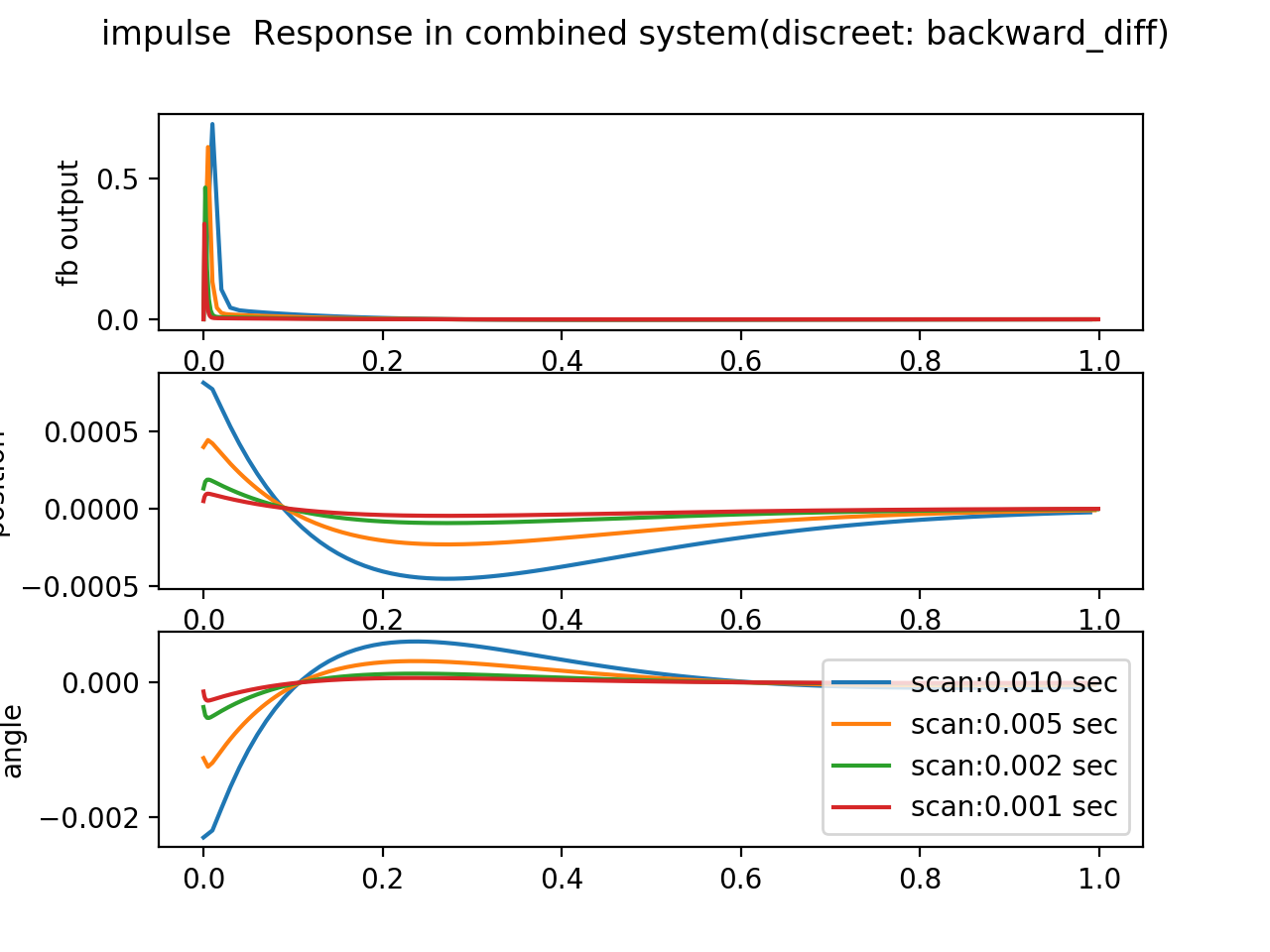
計算機制御でこの制御を実行するためには、離散化の手続きが必要です。離散化の方法を変えた時の、システムのステップ応答の違いをみてみます。 ここでは、python control modduleがサポートする zoh, euler, bilinear, backward-diff の四つの場合について結果を示します。 それぞれの図には、サンプリングの周期を変えた場合の結果を合わせて表示しています。 最も単純でかつmatlabでもpython control でもdefaultのアルゴリズムである zoh が悪くありません。 backward-diff の結果もよく似ています。 bilinear の結果は、制御信号に振動がみられます。 euler は話になりません[9]。 ということで、2019年9月26日現在のパラメータは``backward-diff``を採用しています。

[9]	サンプリングの時間が十分に短ければ、euler(gbt alpha=0)も安定した結果を与える。 Ts=0.01程度では、この問題に対してeulerは安定なシステムを与えない。アルゴリズムの問題なのか、python controlの実装上の問題なのかは未調査。

図. 1.7 離散化アルゴリズムとして zoh(zero-order hold) を使った場合のシステムのステップ応答

図. 1.8 離散化アルゴリズムとして euler(gbt alpha=0) を使った場合のシステムのステップ応答

図. 1.9 離散化アルゴリズムとして bilinear(gbt alpha=0.5) を使った場合のシステムのステップ応答

図. 1.10 離散化アルゴリズムとして backward_diff(gbt alpha=1.0) を使った場合のシステムのステップ応答

1.7. まとめ

倒立振り子を例として、状態推定器付き状態フィードバックによるレギュレータの構成と設計法の概略を示した。Octave（やMatlab, python)を使うことで、 これらの設計法がより身近なものとなりました。

EPICSを用いて、倒立振り子装置を実際に制御してみました。 結果は線型のシミュレーション結果と定性的にはよく一致しています。 今回は状態方程式で使われる、振り子の重さや、慣性モメントなどの定数は文献 [A-3]のものを用いています。 この装置はほとんど手作りであることを考えると、これらの定数も実測値のもとづいたものを使えば、よりシミュレーションと測定値の比較に意味が出るでしょう。 これらの定数を、システム同定の手法を用いて同定する事で、安定性／制御性の向上が図れるでしょう[10]。

[10]	システム稼働中にAIなどの技術を応用して、これらのシステム定数の同定を同時に行うことも考えられます。時間的にゆっくりと変化するドリフトにも 対応できるようになると考えられます。

制御理論としては、此処で採用した線型理論の状態推定器による制御則より進んだ制御方式として、 H∞理論などのロバスト制御や、非線型性や時間ドリフトの影響を取り除くための、適応制御などの方式が知られています。 これらの制御方式は、加速器制御にたいしても有効な方法となり得ます。これらの最新の制御方式の検討を続け、テストベンチとしてこの装置を利用することも期待されます。 動的に繰り返し周波数を変更する、あるいは適応制御的にフィードバックパラメータそのものを変更することを考えると、 c2d()や lqr()相当のルーチンを VxWorks上で用意する必要がある。 すでに LAPACKのサブセットである、 LAPACK-liteは VxWorks上で稼働の実績があるので、これらのルーチンを入手あるいは開発することが必要である。 これらは今後の課題である[11]。

[11]	KEKB,J-PARCなどの加速器制御で使われるIOCのOSの主流はLinuxベースのものになっています。これらのルーチンを使った動的最適化を実現することの障壁はなくなったとも言えるでしょう。

参考文献

[A-1]

Python control module. web page. URL: http://python-control.readthedocs.io/en/latest/intro.html#some-differences-from-matlab.

[A-2]

インターフェース編集部編. “技術者のための UNIX系 OS入門、第八章 RT-Linuxによる倒立振り子の制御''. CQ出版社、東京, 2000.

[A-3]

(1, 2, 3) 川谷亮治他. “倒立振り子キットマニュアル ”.

[A-4]

L. Dalesio. Epics home page. URL: http://www.aps.anl.gov/epics/.

[A-5]

(1, 2, 3, 4) 川谷亮治. 線形制御理論テキスト. URL: http://feedback.nagaokaut.ac.jp/cgi-bin/book.cgi.

[A-6]

W. Stein et al. Sage mathematics software. URL: http://sagemath.org.

[A-7]

野庭建造、西村英和、平田光男. MATLABによる制御系設計. "東京電気大学出版局", 1998.

[A-8]

片山　徹. “線型システムの最適制御 \UTF 2013デスクリプタシステム入門 \UTF 2013”. 近代科学社,東京, 1999. 状態方程式を拡張したデスクリプタシステムの最適制御についての教科書であるが、線型システムの LQ最適フィードバックなどの解法についても詳しい。.

[A-9]

福井大学、川谷研究室. 様々な倒立振子系に対する安定化制御. web page. URL: http://mech.u-fukui.ac.jp/~Kawa-Lab/kenkyu/pend/pend.htm.