Welcome to SAD/FFS & SADScript
SAD/FFS SADScript Version: 1.1.6.7k64, Updated: 6/2/2019
Please use browser's search to find out an item.
The FFS commands are shown in uppercases. The minimum abbreviated form of each command is
enclosed
in (). Each command can be shorten down to that. The optional arguments for the commands a
re usually
shown in [].
The notation ===> reads "equivalent to" below.
Back to SAD Home Page
SAD/FFS Examples
ABORT
APPEND(APP)
ATTRIBUTE(ATTR)
beam-line
beam-line-functions
BeamLine
BeamLineName
ExtractBeamLine
PrintBeamLine
WriteBeamLine
orientation-of-an-element
BYE
character-string
FromCharacterCode
StringFill
StringJoin
StringLength
StringMatchQ
StringPart
StringPosition
StringReplace
StringTrim
Symbol
ToCharacterCode
ToExpression
ToString
command-syntax
components
constants
CALCULATE(CAL)
CHROMATICITY(CHRO)
CLOSE(CLO)
COUPLE(COUP)
data-structure
Extract
Head
Length
List
Part
defining-functions
dynamics
independent-variable
Lagrangean
Hamiltonian
remarks-on-dynamics
x-y-coupling
extended-Twiss-parameters
definitions
DISPLAY(DISP)
ACCELERATION(A)
ALL
BEAM(B)
DUMPOPTICS(D)
GEOMETRY(G)
OGEOMETRY(OG)
ORBIT(O)
pattern-string
PHYSICAL(P)
region
RMATRIX(R)
Z
DRAW
Draw$Option
DUMP
elements
APERT
BEND
AE1
AE2
ANGLE
DISFRIN
DISRAD
DROTATE
DX
DY
E1
E2
F1
FB1
FB2
FRINGE
K0
K1
L
ROTATE
transformation:BEND
CAVI
DISFRIN
DPHI
DVOLT
DX
DY
FREQ
HARM
L
PHI
ROTATE
V02
V1
V11
VOLT
COORD
default-keyword
DECA
DISFRIN
DISRAD
DX
DY
K4
L
ROTATE
transformation:THIN
DODECA
DISFRIN
DISRAD
DX
DY
K5
L
ROTATE
transformation:THIN
DRIFT
L
RADIUS
transformation:DRIFT
keywords
MARK
OFFSET
MULT
AE1
AE2
ANGLE
DISFRIN
DISRAD
DPHI
DVOLT
E1
E2
F1
F2
FB1
FB2
FREQ
FRINGE
HARM
K0
K1
K10
K11
K12
K13
K14
K15
K16
K17
K18
K19
K2
K20
K21
K3
K4
K5
K6
K7
K8
K9
L
misalignments
multipole_with_nonzero_ANGLE
PHI
RADIUS
SK0
SK1
SK10
SK11
SK12
SK13
SK14
SK15
SK16
SK17
SK18
SK19
SK2
SK20
SK21
SK3
SK4
SK5
SK6
SK7
SK8
SK9
VOLT
OCT
DISFRIN
DISRAD
DX
DY
K3
L
ROTATE
transformation:THIN
QUAD
DISFRIN
DISRAD
DX
DY
F1
F2
FRINGE
K1
L
ROTATE
transformation:QUAD
SEXT
DISFRIN
DISRAD
DX
DY
K2
L
ROTATE
transformation:THIN
SOL
BOUND
BZ
DISFRIN
DPX
DPY
DX
DY
F1
GEO
expression
(-)
(/)
AddTo(+=)
Alternatives(|)
And(&&)
Apply (@@)
CompoundExpression(;)
Decrement(--)
DivideBy(/=)
Dot(.)
Equal(==)
Function(&)
Greater(>)
GreaterEqual(>= or =>)
Increment(++)
Less(<)
LessEqual(<= or =<)
List({})
Map (/@)
MapAll(//@)
Member(@)
MessageName(::)
Not(~)
Or(||)
Part([[]])
PatternTest(?)
Plus(+)
Power(^)
Repeated(..)
RepeatedNull(...)
ReplaceAll(/.)
ReplaceRepeated(//.)
Rule(->)
RuleDelayed(:>)
SameQ(===)
Sequence([])
Set(=)
SetDelayed(:=)
StringJoin (//)
SubtractFrom(-=)
TagSet(/:)
Times(*)
TimesBy(*=)
Unequal(<>)
UnsameQ(<=>)
Unset(=.)
ELSE
ELSEIF
EMITTANCE(EMIT)
END
ENDIF
EXECUTE(EXEC)
EXPAND
flags
ABSW
BIPOL
CALC4D
CALC6D
CELL
CMPLOT
COD
CODPLOT
CONV
CONVCASE
DAMPONLY
DAPERT
DIFFRES
ECHO
EMIOUT
FFSPRMPT
FIXSEED
FLUC
GAUSS
GEOCAL
GEOFIX
HALFRES
IDEAL
INS
INTRA
INTRES
JITTER
LOG
LWAKE
MOVESEED
PHOTONS
POL
PRSVCASE
PSPAC
QUIET
RAD
RADCOD
RADLIGHT
RADPOL
RADTAPER
REAL
RELW
RFSW
RING
SELFCOD
SORG
SPAC
STABLE
SUMRES
TRPT
TWAKE
UNIFORM
UNIPOL
UNSTABLE
WSPAC
functions
Data-Manipulation
Fit
FitEmit
FitGaussian
NIntegrate
PolynomialFit
Spline
DownhillSimplex
functional-operations
Apply
Cases
DeleteCases
Difference
FixedPoint
FixedPointList
level-spec
Map
MapThread
Position
Scan
ScanThread
SelectCases
SwitchCases
Thread
FFS-dedicated-functions
AccelerateParticles
BeamMatrix
DynamicApertureSurvey
Element
key-strings:Element
Emittance
ExternalMap
FFS
FFS$SHOW
FitValue
FitWeight
GeoBase
LINE
key-strings:LINE
OptimizeOptics
OrbitGeo
RadiationField
RadiationSpectrum
SetElement
SurvivedParticles
SymplecticJ
SynchroBetaEmittance
TouschekLifetime
TrackParticles
Twiss
VariableRange
VariableWeight
WakeFunction
Graphics
BeamPlot
ColumnPlot
FitPlot
GeometryPlot
HistoPlot
ListContourPlot
ListDensityPlot
ListPlot
OpticsPlot
Plot
Input/Output
$FORM
$Input
$Output
Close
OpenAppend
OpenRead
OpenWrite
PageWidth
Print
Read
ReadString
StandardForm
StringToStream
Write
WriteString
Multiprocessing
Fork
OpenShared
Shared
SharedSize
Object-oriented-programing
Class
Random-number-functions
Random
GaussRandom
ParabolaRandom
SeedRandom
ListRandom
System-interface
System
TemporaryName
Utilities
DateString
MemoryCheck
TimeUsed
Timing
TracePrint
FIT
FITPOINTS(FITP)
FIX
FREE
default-keyword
geometric-functions
GEO
GO
IF
INPUT(IN)
machine-error-commands
matching-function-commands
multi-turn-tracking
MATRIX(MAT)
MEASURE(MEA)
off-momentum-matching
optical-functions
ORG
OUTPUT(OUT)
pattern
MatchQ
physical-constants
PRINT(PRI)
QUIT
RADINT
READ
RECOVER(REC)
REJECT(REJ)
REPEAT(REP)
RESET
REVERSE(REV)
set-value-of-element
keywords
default-keyword
special-variables
$Line
CASE
CHARGE
CONVERGENCE
DAPWIDTH
DP
DP0
DTSYNCH
EFFRFFREQ
EFFVC
EFFVCRATIO
ElementValues
EMITX
EMITXE
EMITY
EMITYE
EMITZ
EMITZE
ExponentOfResidual
FFS$NumericalDerivative
FitFunction
FSHIFT
GCUT
InitialOrbits
LOSSAMPL
LOSSDZ
MatchingAmplitude
MatchingResidual
MASS
MINCOUP
MOMENTUM
NBUNCH
NetResidual
NP
NPARA
OffMomentumWeight
OMEGA0
OpticsEpilog
OpticsProlog
PBUNCH
PhotonList
PHICAV
SIGE
SIGZ
SpeedOfLight
StabilityLevel
STACKSIZ
TITLE
SAVE
SEED
SHOW
SPLIT
STATUS(STAT)
STOP
TERMINATE(TERM)
TYPE(T)
UNTIL
USE
VARIABLES(VAR)
VARY
VISIT
wildcards
Terminates SAD immediately.
See also:
STOP QUIT SAVE USE VISIT BYE
APP {filename | file-number} switches the output stream to the specified file or the
file number.
The output is appended to the existing file.
See also:
TERMINATE(TERM) CLOSE(CLO) INPUT(IN) READ OUTPUT(OUT) END
Usage: ATTR element-pattern
prints out the current value, minimum and maximum values, COUPLEd element and its coeffici
ent for
elements which match the element-pattern.
See also:
COUPLE(COUP) set-value-of-element wildcards
A beam line is defined in the MAIN level by LINE command as:
LINE a = ( [n1*][-]l1 [ [n2*]l2 ...] ) [b = ( ... )];
where l1, l2 are either an element or a line. n1, n2 are positive integers to repeat the s
ame element.
An optional negative sign in fromt of element means the negative orientation of the elemen
t of the
line. A negative orientation of a line is inherited by its elements.
The first element of a beam line must be a MARK element, if it is used by FFS, USE, VISIT
.
Please do not confuse the LINE command in the MAIN level with the LINE function in FFS.
A beam line can be accessed within FFS via beam-line-functions as shown below.
See also:
elements orientation-of-an-element USE VISIT
-
Functions/objects to construct/edit beam lines and elements in FFS.
-
Usage: BeamLine[e1, e2, ...];
where e1, e2 has a form of
[ - ][ n* ] x ,
with x being one of
1) a name (either a symbol or a character string) of an element defined in MAIN.
2) a name (either a symbol or a character string) of a LINE defined in MAIN.
3) a BeamLine object.
An optional negative sign specifies the direction and a number n the repetition number in
the same
way as MAIN. A BeamLine object is automatically expanded to the lowest level whenever it i
s evaluated.
Editing of BeamLine can be done using any List-handling functions such as Join, Insert, De
lete, etc.
of FFS.
A BeamLine object can be used for FFS calculation when it is used as the
argument of USE or VISIT commands:
Examples:
1) USE BeamLine[IP,QF,QD]
2) aaa=ExtractBeamLine[];
USE Join[aaa,-aaa]
In these cases the new beam line becomes a new LINE in the MAIN level, with a name which
is created
automatically.
See also:
ExtractBeamLine PrintBeamLine WriteBeamLine USE VISIT
-
BeamLineName[] returns the name of the current beam line. If a BeamLine object is use
d by USE or
VISIT, the new beam line becomes a new LINE in the MAIN level, with a name which is create
d automatically.
-
Usage: ExtractBeamLine[line]
returns a BeamLine object which represents the expanded form of line which has been define
d in MAIN.
If line is omitted, the current line is assumed.
See also:
BeamLine PrintBeamLine WriteBeamLine USE VISIT
-
Usage: PrintBeamLine[b1,.. ,option]
writes the BeamLine b1,.. to stdout. If b1.. is omitted the current beam line is assumed.
If Format->"MAIN"
is given, it writes in the MAIN-input format. If Name->{name1,..} is given, names of BeamL
ines are
also written. The number of Name must be not smaller than number of BeamLines.
See also:
BeamLine ExtractBeamLine WriteBeamLine USE VISIT
-
Usage: WriteBeamLine[f, b1,.. ,option]
writes the BeamLine b1,.. to file f. If b1.. is omitted the current beam line is assumed.
If Format->"MAIN"
is given, it writes in the MAIN-input format. If Name->{name1,..} is given, names of BeamL
ines are
also written. The number of Name must be not smaller than number of BeamLines.
See also:
BeamLine ExtractBeamLine PrintBeamLine USE VISIT
-
An element with negative orientation means a reversal of the element along the z-axi
s. Thus all
magnets except for a solenoid does not change the polarity. A solenoid changes the polarit
y. An RF
cavity should change, however, it does not in the current implementation. The edge angles
and fringe
parameters of the entrance and the exit swap.
AX, AY, AZ, EPX, EPY, ZPX, ZPY, R2, R3 of a MARK element are reversed.
The orientation is printed out by DISP. It can be accessed by LINE["DIR"] .
See also:
beam-line LINE
Exits from the current beam line and returns to the original beam line where VISIT co
mmand was issued.
All information specific to the beam line, such as matching conditions are restored.
Note that BYE does neither SAVE the values of elements of the leaving beam line, nor RE
SET the
values of elements of the returning beam line.
See also:
VISIT USE SAVE RESET STOP QUIT ABORT
A character-string is expressed by enclosing in "". Special characters are expressed
using \:
\n new line
\r carriage return
\t tab
\" double quote
\ backslash
\nnn a character whose octal code is nnn.
If a character-string is written over multiple lines, \ must be placed at the end of each
line.
The length of a character-string is limited to 2^31-1.
-
FromCharacterCode[r_Real] returns a character whose character code is r.
FromCharacterCode[l_List] returns a character-string whose character codes are l.
See also:
ToCharacterCode
-
StringFill[s, sf, n] with strings s and sf, n > 0, returns (s//sf//sf...)[1,n] .
StringFill[s, sf, -n] with strings s and sf, n > 0, returns (...sf//sf//s)[-n,-1] .
See also:
StringJoin StringJoin (//) StringPart
-
StringJoin[s1, s2, [,s3...]] ===> s1 // s2 [//s3...] concatenates strings s1, s2 [,s
3...].
See also:
StringJoin (//)
-
StringLength[s] returns the length of string s.
-
StringMatchQ[s, spat] returns True/False whether string s matches string-patten spat.
See also:
wildcards
-
s_String[n] returns the n-th character in s.
s_String[n1, n2] returns the substring from n1-th through n2-th characters of s.
If n1, n2 are negative, they count from the end of the string.
-
StringPosition[s, subs] returns a list of positions of subs in string s.
StringPosition[s, subs, n] returns a list of first n positions of subs in string s.
Example: StringPosition["abcbcbcbcb","bcb"] returns {{2,4},{4,6},{6,8},{8,10}}.
-
StringReplace[s, rules] replaces the parts of string s accoding to rules, which is a
Rule or a list
of Rules:
StringReplace["abcbcbcbc","bcb"->"xyx"] ===> "axyxcxyxc"
StringReplace["abcbcbcbc",{"bcb"->"xy","cbc"->"pqrs"}] ===> "axypqrsbc" .
-
StringTrim[s] removes the leading and trailing spaces and tabs from s.
-
Symbol[s] returns a Symbol whose name is character-string s.
-
ToCharacterCode[s] returns the list of character codes of character-string s.
See also:
FromCharacterCode
-
ToExpression[s] converts a character-string s to an expression and evaluate it.
See also:
ToString
-
ToString[expr] evaluates an expression expr, then converts to a character-string.
ToString[expr, [FormatType ->] form [, form1...]] converts expr using one or more formats
form [,form1...].
Available formats are:
InputForm special characters are quoted with \.
HoldForm converts expr without evaluation.
StandardForm converts with the standard number format and PageWidth.
GenelicSymbolForm do not display the generation ($nnn) of local symbols for Module.
See also:
$FORM PageWidth StandardForm Module ToExpression
The command syntax in FFS is
expression1 [param1..] [;] expression2..
(1) The input is first evaluated as an expression. If the expression returns a Symbol wit
h the same
name as the expression itself, it is interpreted as an FFS command, otherwise the ret
urned value
is printed out unless it is Null.
(2) Each command takes succeeding its parameters if necessary. A command with indefinite
number
of parameters can be terminated by semicolon. Most commands terminate itself at the e
nd of line.
(3) A line can be continued to the next line if a backslash is placed at the end of the l
ine.
(4) An expression continues to the next line if it is not closed in the line.
(5) An exclamation mark comments out the rest of the line.
Example: A command line
QF* .1
means the set-value-of-element command as unless the symbol QF has been defined otherwise.
If QF
has been defines as a number, such as QF=2.5, the above command line is interpreted as Tim
es[QF,.1]
then returns .25 .
See also:
expression functions
Components are the objects which consist the beam line. A component simulates an indi
vidual magnet,
drift space, or rf-cavity. The parameters of a component is specified the values in the co
rresponding
element with the same name as the component, which simulates a power supply. Many componen
ts can
be attached to the same element. Parameters of each component may deviate from the corresp
onding
element if machine errors are given.
A component is specified with the form name[.order][{+-}offset], where name is the name
of the
component. The number order means the order-th component which belongs to name element, co
unted from
the beginning of the line starting from 1. Offset is a positive or negative number to spec
ify the
downstream or upstream components from the given component. If order is omitted, the first
element
is assumed, and if offset is omitted, zero is assumed.
The end of line is specified by $$$. The first component can be specified by ^^^.
See also:
elements
There are pre-defined special symbols for constants in FFS:
symbol value
True 1
False 0
Infinity INF
INF INF
NaN NaN
Pi ArcSin[1]*2
E Exp[1]
I Complex[0,1]
Degree Pi/180
GoldenRatio (1+Sqrt[5])/2
EulerGamma 0.57721566490153286061
See also:
special-variables physical-constants flags expression
Usage: (1) CAL [[NO]EXPAND]]
(2) CAL matching-function1[-] [matching-function2[-]..]
(1) With no argument or with an option [NO]EXPAND, calculates the optics and the matching-
functions
using the current values of the components. It prints out the values of the matching-funct
ions specified
either by the matching-function-commands or the second usage of CAL, as described below. I
f an option
EXPAND is given(default), it expands the beam line before the calculation. If NOEXPAND is
given,
it calculates without any expansion. FFS["CAL"] and FFS["GO"] returns the result as a li
st, whose
format is
{dp, kind, reslist, function-values},
where
dp: a list contains dp/p0 .
kind: a list of kind of the orbit (usually 0, but 1 to 6 for the finite amplitude matc
hing, see
MatchingAmplitude).
reslist: a list of {residual, xstab, ystab}, where
residual: matching residual,
xstab: True when the matrix is stable in X,
ystab: True when the matrix is stable in Y, for each orbit.
Above are lists with length nf (== number of orbits).
function-values: a list of length nc (== number of calculated items). Each element has the
form:
{component1, component2, function, list-of-values},
where
component1, component2: fit locations (see FIT).
function: name of the function (see matching-function-commands).
list-of-values: list of the value of the function for each orbit Length nf.
The central orbit comes at the Floor[(n+1)/2]-th element.
(2) With matching-function names, sets the matching-functions at the current fit point to
be printed
out after calculation. If the matching-function is followed by a minus sign, it suppresses
the print-out.
\nExample:
CALC BX BY CAL
See also:
GO DISPLAY(DISP) COUPLE(COUP) ATTRIBUTE(ATTR) SHOW FIT matching-function-commands EXPAND
CONV CONVERGENCE MatchingResidual FFS
CHRO prints out the chromaticity of QUAD and SEXT in the entire beam line using the s
implest formula:
xi_{x,y}=Integrate[-(K1/L) beta_{x,y}(s) ds] for QUAD,
xi_{x,y}=Integrate[-(K2/L) eta_x (s) beta_{x,y}(s) ds] for SEXT.
These formula are not valid when there is x-y coupling or vertical dispersion.
CLOSE [INPUT(IN)] closes the current input stream and switches it to the previous
input stream.
CLOSE OUTPUT(OUT) suspends the current output and switches it to the previous output str
eam.
See also:
TERMINATE(TERM) INPUT(IN) READ OUTPUT(OUT) APPEND(APP) END
Usage: COUP slave-element master-element coefficient
sets the value of the default-keyword of slave-element to be equal to coefficient times th
e value
of the default-keyword of master-element. COUPLE(COUP) cannot be cascaded. The master-elem
ent cannot
be COUPLEd to any other element. To reset COUPLE, say COUP slave-element slave-element 1.
Consider ElementValues to define universal coupling for any keywords.
See also:
ATTRIBUTE(ATTR) FREE ElementValues
All data and "programs" in SAD Script are expressed either by an atom or a list-struc
ture:
head[body1 [,body2...]]
where head and body1... are atom or list-structure. Defined atoms are:
Real a real number
Symbol a symbol
String a character-string
Pattern a pattern structure for argument matching
Currently the lengths of a list-structure, a character-string, and the name of a symbol ar
e limited
to 2^31-1. A real number has an accuracy of 8 bytes.
See also:
character-string pattern
-
Extract[f, part [,head]]
takes elements specified by part, which is a list of indices or Null. Optional head is app
lied at
each element before evaluation.
Example: Extract[{a,b,c,d,e},{3}] returns c
Extract[{a,b,c,d,e},{3,4}] is an error
Extract[{a,b,c,d,e},{{3},{4}}] returns {c,d}
Extract[Hold[{a,b,c,d,e}],{1,3}, Hold] returns Hold[c]
See also:
Part
-
Head[f] takes the head of an expression f.
-
Length[f] returns the number of elements in the body of a structure f.
-
List is a special symbol to be the head of generic list-structure.
List[a, b, c, ...] is represented as {a, b, c, ...}.
A list is also used to represent a mathematical vector and matrices.
Most of mathematical functions are operated at each element of a list.
-
Part[f, a [,b ,...]] ===> f[[a, [,b ...]]]
takes the a-th element of structure f. f[[a, b]] is equivalent to f[[a]][[b]].
If a is zero, it takes the head of f.
if a is negative, f[[a]] os equivalent to f[[Length[f] + 1 + a]].
If a is a list of Reals {a1, a2, ...}, f[[a]] returns {f[[a1]], f[[a2]], ...}.
If a is Null, f[[,b]] is returns {f[[1,a]], ..., f[[Length[f], b]]}.
See also:
Length Head Extract
A function is defined by one of the following forms:
f[pat1 [,pat2...]] (:)= body;
f[pat1 [,pat2...]] ^(:)= body;
g//:f[pat1 [,pat2...]] (:)= body;
where pat1 [,pat2...] are patterns (including expressions).
If UpSet(^=) or UpSetDelayed (^:=) is used, the definition is associated with the symbol
in the
first level of l.h.s.
If TagSet(//:) is used, the definition is associated with the symbol on the left of //: .
The patters can be an expression including constants. The definition with constant argume
nts can
be accessed faster than searching a list, in general, so they are suitable for a data base
. Definitions
with constant arguments have higher priorities than with patterns.
See also:
UpSet UpSetDelayed TagSet(/:) pattern
-
See also:
Lagrangean Hamiltonian
-
See also:
Hamiltonian independent-variable
-
See also:
Lagrangean independent-variable
-
See also:
Hamiltonian
-
See also:
DISPLAY(DISP) optical-functions matching-function-commands
-
A symplectic matrix such as the normal mode matrix can be expressed in terms of the e
xtended Twiss
parameters. In 6 by 6 case, those are
AX BX ZX EX
PSIX ZPX EPX
R1 R2 AY BY ZY EY
R3 R4 PSIY ZPY EPY
AZ BZ
PSIZ .
A(X,Y,Z), B(X,Y,Z) are alphas and betas in the usual sense, after a diagonalization to 2 b
y 2 submatrices.
PSI(X,Y,Z) are the rotation angle to set one the coordinate to parallel to the (X,Y,Z) axe
s. R(1,2,3,4)
are the components of the x-y coupling matrix (see x-y-coupling). E(X,PX,Y,PY) are "disper
sions"
which decouples synchro-beta coupling terms together with Z(X,PX,Y,PY). Those parameters s
hould agree
with what FFS calculates in the case of no synchro-beta couplings.
See also:
x-y-coupling optical-functions
Usage: DISP_LAY [keywords] [pattern-string] [region]
Displays values of various optical-/geometric-functions at the components given by the pat
tern-string
in the region (see region) in the current beam line. It has several display modes specifie
d by the
keywords. As the default, it displays AX, BX, NX, EX, EPX, AY, BY, NY, EY, EPY, LENG, the
length
and the value of the default-keyword of the component. Each line refers to the entrance of
each component
of the line. The end of the beam line has the name "$$$". The first component can be speci
fied by
"^^^".
DISP does not calculate the functions to be displayed, so CALCULATE(CALC) is necessary
whenever
values of components are updated.
See also:
TYPE(T) optical-functions geometric-functions
-
DISP A displays the nominal energy, energy deviation(DDP), longitudinal position(z),
and emittances
for a transport line with accelerating cavities. The flag TRPT must be on.
See also:
TRPT RING elements CAVI special-variables EMITX EMITY DP
-
ALL is a word to choose the entire beam line for the region to be displayed.
See also:
region pattern-string
-
DISP B displays the beam sizes and the projected Twiss parameters calculated either b
y Twiss parameters
or the EMIT command with the CODPLOT flag.
Example: EMITX=...; EMITY=...;DP=...;
BEAMSIZE(BEAM)
DISP B
See also:
BEAMSIZE(BEAM) EMITTANCE(EMIT) CODPLOT GAUSS UNIFORM special-variables EMITX EMITY DP
-
DISP D displays all matching-functions in one line suitable to be read by a spread-sh
eet program.
See also:
optical-functions geometric-functions matching-function-commands
-
DISP G displays geometric information of the beam line. It shows the geometry at the
coordinate,
except for a SOL region, where the geometry at the orbit is shown.
See also:
geometric-functions matching-function-commands
-
DISP OG displays geometric information at the orbit.
See also:
geometric-functions matching-function-commands
-
DISP O displays the orbits DX, DPX, DY, DPY together with the other
optical-functions.
See also:
optical-functions matching-function-commands
-
The components in the current region can be selectively displayed by the DISP command
using the pattern-string.
The pattern-string is a character string involving the wildcards to match the name of the
components.
Note that the components are chosen in the current region, and the keyword ALL is necessar
y to extend
it to the entire beam line.
See also:
DISPLAY(DISP) wildcards components region ALL
-
DISP P displays the physical dispersions PEX, PEPX, PEY, PEP, together with the 1D op
tical parameters.
See also:
optical-functions matching-function-commands
-
Region for DISPLAY(DISP) is specified as
DISP .... begin [end]
with begin and end having the form name[.order][{+-}offset] (see components).
Example: DISP ... QF.2-10 QD+5
displays functions starting at 10 elements upstream from the entrance of the second QF thr
ough 5
elements downstream from the entrance of the first QD. The region for DISP is kept after o
nce set.
It is shown in the second part of the prompt when FFSPRMPT is ON, and also seen by the STA
TUS(STAT)
command.
The components which match the pattern-string in DISP are only chosen in the current regi
on.
See also:
ALL pattern-string components STATUS(STAT)
-
DISP R displays the components of the x-y coupling matrix R together with the 1D opti
cal parameters.
See x-y-coupling.
See also:
x-y-coupling optical-functions matching-function-commands
-
DISP Z displays muatching functions related to the Z plane: AZ BZ NZ DZ DDP ZX ZPX ZY
ZPY , which
are obtained by CAL/GO with CALC6D.
See also:
extended-Twiss-parameters CALC6D CALC4D
Usage: DRAW [begin end] fun1 [fun2..] [& fun11 [fun12..]] [element-pattern]
draws a plot of optical functions in multi columns. It calls OpticsPlot internally. Availa
ble functions
are all matching-functions (except LENG, TRX, TRY, GX, GY, GZ, CHI1, CHI2, CHI3) and addit
ional functions.
If functions are separated by ampersand (&), these are plotted in a separated window.
If begin- and end-components are specified, the plot region is limited between them. If
the end-component
comes earlier than the begin-components, it wraps the plot around the beam line.
If the optional element-pattern is given, it draws the beam-line lattice with the labels
for elements
which match element-pattern. If LAT is specified for element-pattern, the lattice is drawn
without
label.
A character string assigned to TITLE is shown as the FrameLabel on the top of the plot.
Example:
TITLE="FCCee_t_202_nosol_16_ipac.sad";
Draw$Option={Thickness->2};
DRAW BX BY & EX EY Q*;
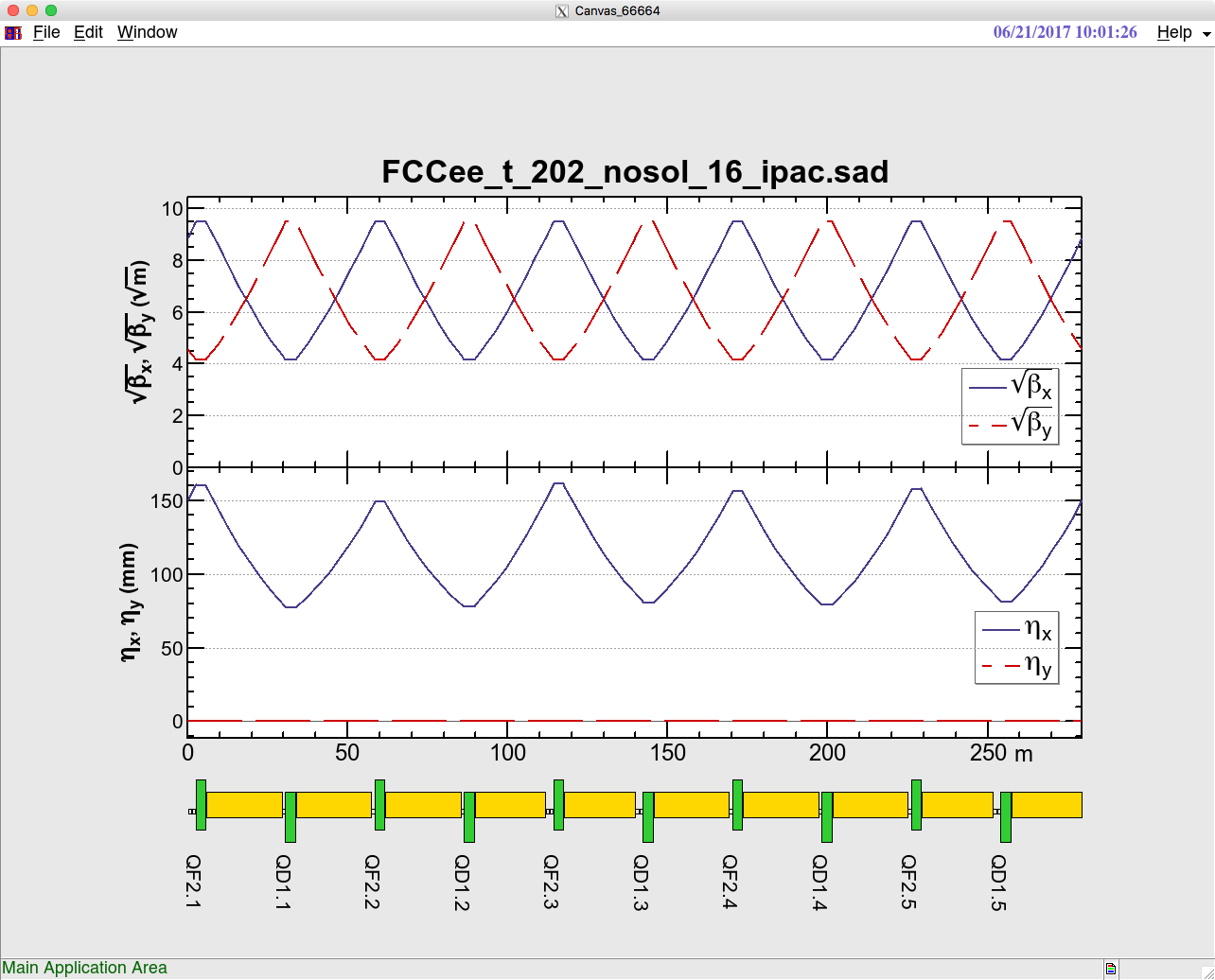
See also:
OpticsPlot special-variables TITLE matching-function-commands OUTPUT(OUT) TERMINATE(TERM)
GEO DISPLAY(DISP) wildcards
-
Draw$Option is a list of rules to specify Graphics options for the entire DRAW. If y
ou need option
for each column, use OpticsPlot
See also:
DRAW OpticsPlot Graphics
Usage: DUMP component-pattern [component-pattern1..]
prints out the current machine errors of components which match component-pattern.
See also:
machine-error-commands components wildcards
An element in FFS represents an object which has a unique name and several keywords w
ith values.
This simulates a power supply of a magnet. An element has one or more components, which co
rrespond
to individual magnets in a beam line. Each component may have different values from the va
lues of
the corresponding element. This simulates the machine error which varies magnet to magnet
The value of an element can be saved to or recovered from the element-save-buffer by SA
VE or RESET
commands. Different beam lines can share the same element, and their values can be differe
nt to each
other, but they have the common element-save-buffer. Therefore the value of an element can
be transferred
between beam lines by SAVE and RESET command through the element-save-buffer.
An element is created only in SAD MAIN level. In the definition, if a keyword is omitte
d, the
previous definition is unchanged. All keywords have the default value zero. In FFS, it is
only possible
to change their values.
See also:
TYPE(T) set-value-of-element Element
-
An aperture. Only valid in tracking. A particle with
can pass through the aperture, otherwise it is lost and a message is printed out. If AX or
AY is
zero (default), they are interpreted as infinity. If AX <=> 0 && AY <=> 0 and (DX1 == DX2
or DY1
== DY2) then the aperture is only determined by AX and AY.
-
A bending magnet.
-
The absolute face angle at the entrance. The effective face angle is E1 * ANGLE + AE1
, and a positive
angle at the entrance corresponds to a surface with dx/ds > 0.
See also:
E1 AE2 ANGLE
-
The absolute face-angle at the exit to the bending angle. The effective face angle is
E2 * ANGLE
+ AE2, and a positive angle at the exit corresponds to a surface with dx/ds < 0.
See also:
E2 AE1 ANGLE
-
The bending angle. If positive, it bends the orbit in x-s plane toward negative-x-dir
ection. ANGLE
determines the geometry of the beam line, while K0 represents a dipole kick on top of the
bending
angle given by ANGLE, i.e., the total deflection of the beam is given of ANGLE + K0.
See also:
K0
-
If nonzero, the nonlinear Maxwellian fringe is suppressed.
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Additional rotation in x-y plane to simulate a rotation error. DROTATE does not affec
t the geometry
of the ring.
See also:
DX DY ROTATE
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
The ratio of the face-angle at the entrance to the bending angle. The effective face
angle is E1
* ANGLE + AE1, and a positive angle at the entrance corresponds to a surface with dx/ds >
0. For
example, a symmetrically-placed rectangular magnet has
E1 = 0.5 and E2 = 0.5.
See also:
AE1 E2 ANGLE
-
The ratio of the face-angle at the exit to the bending angle. The effective face angl
e is E2 * ANGLE
+ AE2, and a positive angle at the exit corresponds to a surface with dx/ds < 0. For examp
le, a symmetrically-placed
rectangular magnet has E1 = 0.5 and E2 = 0.5.
See also:
AE2 E1 ANGLE
-
Length of the slope of the field at the edge as:
By(s) | *******
| *
| *
|*
*
*|
* |
* |
----*******---+--------- s
| |
|<----->|
| F1 |
Only the effects up to y^4 in Hamiltonian are taken into account. A more rigorous definiti
on is
where integration is done over one fringe.
The transformation of the linear fringe of the entrance of a bend is
where f is the length of fringe given by F1, and rhob bending radius at the design momentu
m. At the exit, the sign of rhob is changed. This linear fringe also changes the path leng
th in the body of the bend as
to maintain the geometric position of the design orbit, i.e., you have to increase the ben
d field
a little bit to keep the orbit unchanged. Unlike a quadrupole, the effect of linear fringe
is always
applied at both the entrance and the exit, otherwise you cannot obtain a circular design o
rbit.
Use FB1 and FB2 to specify the values of entrance and exit separately.
See also:
FRINGE FB1 FB2
-
F1 at the entrance. Actually F1 + FB1 is used at the entrance.
See also:
F1 FB2
-
F1 at the exit. Actually F1 + FB2 is used at the exit.
See also:
F1 FB1
-
When FRINGE is non-zero, the effect of the linear fringe F1 is taken into account bot
h at the entrance and the exit.
The transformation of the linear fringe of the entrance of a bend is
where f is the length of fringe given by F1, and rhob bending radius at the design momentu
m. At the exit, the sign of rhob is changed. This linear fringe also changes the path leng
th in the body of the bend as
to maintain the geometric position of the design orbit, i.e., you have to increase the ben
d field
a little bit to keep the orbit unchanged. Unlike a quadrupole, the effect of linear fringe
is always
applied at both the entrance and the exit, otherwise you cannot obtain a circular design o
rbit.
Use FB1 and FB2 to specify the values of entrance and exit separately.
See also:
F1
-
The normal 2-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 4-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length along the arc of the orbit.
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
The transformation of a bend depends on the value of K1. If K1 is zero, it is a serie
s of transformations:
(transformation due to misalignments)
(drift to the entrance face)
(linear fringe at entrance face)
(nonlinear fringe at entrance)
(body of bend)
(nonlinear fringe at exit)
(linear fringe at exit face)
(drift from the exit face)
(transformation due to misalignments)
If K1 is nonzero, the effects from E1 and E2 are approximated by thin
quadrupoles. Then the body is subdivided into
1 + floor(sqrt(abs(K1 L')/(12 10^-5 EPS)))
pieces (EPS = 1 is used when EPS = 0), and the bend-body transformation above is done for
each piece
and the kick from K1 is applied alternatively. In FFS optics and Emittance calculations, o
r when
the synchrotron radiation is turned on, the same algorithm as K1 <> 0 is applied.
See also:
coordinates
-
Accelerating structure.
-
If nonzero, the Maxwellian fringe is suppressed. The effects of DISFRIN and FRINGE ar
e summarized
as
DISFRIN=0 DISFRIN<>0
FRINGE=0 entr & exit none
FRINGE=1 entr none
FRINGE=2 exit none
FRINGE=3 entr & exit none
See also:
FRINGE
-
Relative phase offset. The stable synchrotron phase above the transition is near PHI
= 0. The acceleration is given by
where ts is the equilibrium time determined by the valance between the acceleration and th
e radiation
loss around the ring. DPHI is not taken into account to determine the design momentum p0(s
).
See also:
FREQ VOLT DVOLT V1 V20 V11
-
Additional accelerating voltage to be added to VOLT without affecting the design momentum.
See also:
VOLT
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
Rf frequency. If this keyword is nonzero, the keyword HARM is ignored.
See also:
HARM
-
A harmonic number. This is valid only when FREQ is zero.
See also:
FREQ
-
The effective length.
-
Relative phase offset. The stable synchrotron phase above the transition is near PHI
= 0. The acceleration is given by
where ts is the equilibrium time determined by the valance between the acceleration and th
e radiation
loss around the ring.
See also:
FREQ VOLT DVOLT V1 V20 V11
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
The y^2-dependence of the acceleration. Tracking only.
See also:
VOLT DVOLT V1 V20 V11
-
The linear x-dependence of the acceleration. Tracking only.
See also:
VOLT DVOLT V1 V11 V02
-
The xy-dependence of the acceleration. Tracking only.
See also:
VOLT DVOLT V1 V20 V02
-
Accelerating peak voltage in Volt.
where ts is the equilibrium time determined by the valance between the acceleration and th
e radiation
loss around the ring. (CAVI only) The non-relativistic corrections
(VOLT+DVOLT)*(2 Pi FREQ/c)^2/(gamma beta)^2/4 are
automatically added to V20 and V02, respectively. The Lorentz factor is evaluated as inver
se of average
of 1/(beta gamma) at the entrance and the exit.
CAVI includes the edge effect at the lowest order, given by a Hamiltonian at the entran
ce edge
at s0:
Hf = - (e (VOLT+DVOLT)/L)(Sin(omega t - dphi) + Sin(dphi) - offset) (x^2+y^2)/4 delta(s
-s0)
where dphi and offset are determined by the cavity phase and the radiation loss, which is
nonzero
only in the case of NORAD. The sign flips at the exit. This Hamiltonian should be consiste
nt with
what Kiyoshi Kubo derived.
See also:
DVOLT
-
An element for an arbitrary coordinate transformation. This element can be used to ex
press an off-axis element.
Usage: COORD name=(DX=dx DY=dy CHI1=chi1 CHI2=chi2 CHI3=chi3 DIR=dir); .
If dir is zero (default), the transformation of the coordinate by COORD is
and if dir is nonzero,
where {x, y, z}_1 are the new coordinates and
Note that these transformationis are NOT the inverse to each other.
To use this element, you have to calculate the values of those parameters carefully. DI
SP G may
help you but there is no automatic way to get them. You may also have to be careful when y
ou use
a line with this element in the reverse direction.
A better way to do an equivalent thing in most cases is to use SOL. Unlike COORD, SOL a
utomatically
determines the parameters for the coordinate transformation.
See also:
SOL DISPLAY(DISP)
-
The default and available non-default variable keywords are:
type default-keyword non-default variable keyword
DRIFT L -
BEND ANGLE K1,K0,E1,E2
QUAD K1 ROTATE
SEXT K2 ROTATE
OCT K3 ROTATE
DECA K4 ROTATE
DODECA K5 ROTATE
MULT K1 K0,K2..K21,SK0,SK1,SK2..SK21,ROTATE,ANGLE
MARK - AX,BX,EX,EPX,AY,BY,EY,EPY,R1,R2,R3,R4,DETR,
DX,DPX,DY,DPY,DZ,DDP,AZ,BZ,ZX,ZPX,ZY,ZPY
See also:
keywords
-
A decapole magnet.
-
If nonzero, the nonlinear Maxwellian fringe is suppressed.
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
The normal 10-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length.
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
-
A dodecapole magnet.
-
If nonzero, the nonlinear Maxwellian fringe is suppressed.
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
The normal 12-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length.
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
-
A drift space.
-
The length, can be negative.
-
Radius of the vacuum chamber. Effective when SPAC is ON.
See also:
SPAC
-
The transformation of a drift is
with
See also:
coordinates
-
Available keywords are:
type keywords
DRIFT L RADIUS
BEND L ROTATE DROTATE DX DY ANGLE K0 K1 E1 E2 AE1 AE2 F1 FB1 FB2 FRINGE DISFRIN DISRAD
EPS RANKICK
QUAD L ROTATE DX DY K1 F1 F2 FRINGE DISFRIN DISRAD EPS
SEXT L ROTATE DX DY K2 DISFRIN DISRAD
OCT L ROTATE DX DY K3 DISFRIN DISRAD
DECA L ROTATE DX DY K4 DISFRIN DISRAD
DODECA L ROTATE DX DY K5 DISFRIN DISRAD
MULT L DX DY DZ CHI1 CHI2 ROTATE(=CHI3) K0..K21 SK0..SK21 DISFRIN F1 F2 FRINGE DISRAD E
PS VOLT
DVOLT HARM PHI DPHI FREQ RADIUS ANGLE E1 E2 AE1 AE2 DROTATE
SOL BZ DX DY DZ DPX DPY BOUND GEO CHI1 CHI2 CHI3 DBZ DISFRIN
CAVI L ROTATE DX DY VOLT DVOLT V1 V20 V11 V02 FREQ PHI HARM RANVOLT RANPHASE DISFRIN FR
INGE
TCAVI L ROTATE DX DY K0 V1 FREQ PHI HARM RANKICK RANPHASE
COORD DX DY CHI1 CHI2 CHI3 DIR
MARK AX BX AY BY EX EPX EY EPY R1 R2 R3 R4 DETR DX DPX DY DPY DZ DDP AZ BZ NZ ZX ZPX ZY
ZPY EMITX
EMITY DP AZ SIGZ GEO OFFSET
APERT DX1 DX2 DY1 DY2 DP AX AY DX DY
See also:
default-keyword set-value-of-element Element
-
MARK elements play special roles in FFS:
(1) The first element of the beam line must be a MARK element to be used by FFS. In this
case the
MARK element contains the parameters of the incoming beam (see optical-functions, spe
cial-variables
EMITX, EMITY, DP).
(2) The calculated optical parameters at a MARK command is saved by SAVE or STOP commands
, then
it can be used as the incoming condition of other beam lines which have the same MARK
element.
Example: MARK P1 = (EMITX = .. EMITY = .. DP = ..);
LINE A = ( .. P1 ..)
B = (P1 .. );
FFS USE = A;
... do matching on LINE A
SAVE P1 save the parameters at P1
USE B; switch to LINE B
... do matching of LINE B whose entrance is to be
matched P1.
(3) If a MARK element has keyword GEO nonzero, this MARK element becomes the origin of th
e geometric
rotation after the last SOL element.
(4) The values of optical-functions of the MARK element at the beginning of the beam line
can be
specified as matching variables by the FREE command.
A MARK elements have all optical-functions as its keywords except NX, NY, TRX, TRY, and L
ENG. Also
it has keywords EMITX, EMITY, and DP which give the values of the corresponding special-va
riables.
See also:
SAVE USE optical-functions SOL special-variables EMITX EMITY DP
-
OFFSET is a relative position from the current position. A fraction is allowed to spe
cify a location
within an element.
If the MARK at the beginning of a beam line has OFFSET nonzero, the optics calculation
starts
from the shifted location. If the last component of a beam line is a MARK with nonzero OFF
SET, the
optics calculation stops at the shifted location. The periodic condition is applied betwee
n those
shifted locations.
The geometric origin and the origin of LENG shift to the first MARK.
Examples:
(1) LINE A = ( ... QF PQFC ... );
QUAD QF = (L=0.3 K1=0.2);
MARK PQFC = (OFFSET = -0.5);
Here PQFC represents the center of QF.
(2) LINE A = ( ... PQFC QF ... );
QUAD QF = (L=0.3 K1=0.2);
MARK PQFC = (OFFSET = 1.5);
Here PQFC represents the center of QF, too (consider why). The value of OFFSET is interpre
ted taking
the direction of the LINE into account, i.e., a MARK in a line A represents the same locat
ion in
a line -A.
Restrictions:
(1) Function TrackParticles does not take OFFSET into account if the start
or stop location is in the midst of a beam line and a Mark with nonzero
OFFSET, in the current version. Tracking for entire beam line or
MEASURE(MEA) command supports OFFSET.
(2) The outputs by DISPLAY(DISP) outside of the narrowed region by OFFSET are
meaningless.
-
A magnet with multipoles. Note that the reference plane is defined so that the skew q
uadrupole component
becomes zero.
It can have a nonzero ANGLE to express a combined function bending magnet with multipol
es. Note
that the definition of the multipoles with nonzero ANGLE is very special The current versi
on does
not allow nonzero ANGLE inside a solenoid or with acceleration. Also the fringe field and
emittance
calculation are not installed properly for nonzero ANGLE.
See also:
multipole_with_nonzero_ANGLE
-
The absolute face angle at the entrance. The effective face angle is E1 * ANGLE + AE1
, and a positive
angle at the entrance corresponds to a surface with dx/ds > 0.
See also:
E1 AE2 ANGLE
-
The absolute face-angle at the exit to the bending angle. The effective face angle is
E2 * ANGLE
+ AE2, and a positive angle at the exit corresponds to a surface with dx/ds < 0.
See also:
E2 AE1 ANGLE
-
The bending angle. If positive, it bends the orbit in x-s plane toward negative-x-dir
ection. ANGLE
determines the geometry of the beam line, while K0 represents a dipole kick on top of the
bending
angle given by ANGLE, i.e., the total deflection of the beam is given of ANGLE + K0.
See also:
K0
-
If nonzero, the nonlinear maxwellian fringe is suppressed. The effects of DISFRIN and
FRINGE are
summarized as
DISFRIN=0 DISFRIN<>0
Nonlinear Linear Nonlinear Linear
FRINGE=0 entr & exit none none none
FRINGE=1 entr entr none entr
FRINGE=2 exit exit none exit
FRINGE=3 entr & exit entr & exit none entr & exit
See also:
FRINGE
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Relative phase offset. The stable synchrotron phase above the transition is near PHI
= 0. The acceleration is given as
where ts is the equilibrium time determined by the valance between the acceleration and th
e radiation
loss around the ring. DPHI is not taken into account to determine the design momentum p0(s
).
See also:
FREQ VOLT DVOLT V1 V20 V11
-
Additional accelerating peak voltage to be added to Volt, without affecting the desig
n momentum p0(s).
See also:
VOLT
-
The ratio of the face-angle at the entrance to the bending angle. The effective face
angle is E1
* ANGLE + AE1, and a positive angle at the entrance corresponds to a surface with dx/ds >
0. For
example, a symmetrically-placed rectangular magnet has
E1 = 0.5 and E2 = 0.5.
See also:
AE1 E2 ANGLE
-
The ratio of the face-angle at the exit to the bending angle. The effective face angl
e is E2 * ANGLE
+ AE2, and a positive angle at the exit corresponds to a surface with dx/ds < 0. For examp
le, a symmetrically-placed
rectangular magnet has E1 = 0.5 and E2 = 0.5.
See also:
AE2 E1 ANGLE
-
See also:
F2 FRINGE
-
See also:
F1 FRINGE
-
Linear Fringe length F1 for the K0 component at the entrance.
See also:
BEND F1 FB1
-
Linear Fringe length F1 for the K0 component at the exit.
See also:
BEND F1 FB2
-
Rf frequency. If this keyword is nonzero, the keyword HARM is ignored.
See also:
HARM
-
The effects of the linear fringe (characterized by F1 and F2), and the nonlinear Mexw
ellian fringe
are controled as:
DISFRIN=0 DISFRIN<>0
Nonlinear Linear Nonlinear Linear
FRINGE=0 entr & exit none none none
FRINGE=1 entr entr none entr
FRINGE=2 exit exit none exit
FRINGE=3 entr & exit entr & exit none entr & exit
See also:
F1 F2 DISFRIN
-
A harmonic number. This is valid only when FREQ is zero.
See also:
FREQ
-
The normal 2-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 4-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 22-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 24-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 26-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 28-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 30-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 32-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 34-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 36-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 38-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 40-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 6-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 42-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 44-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 8-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 10-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 12-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 14-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 16-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 18-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The normal 20-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length.
-
Misalignments of a MULT element are expressed by the keywords DX, DY, DZ, CHI1, CHI2,
and ROTATE(=CHI3). They specify all misalignments of a rigid body, At the entrance of MU
LT, the coordinates of a particle are transformed as
where c1 and s1 are Cos[CHI1] and Sin[CHI1], etc. The inverse is applied at the exit.
Those misalignments are also valid within a solenoid.
Other straight elements such as QUAD or THIN do not and will not have these full misali
gnment
specifications, because they can be substituted by MULT.
The geometry of the design orbit is determined by the saved values of CHI1, CHI2, and D
Z, while
the current values are used for DX, DY, and ROTATE.
-
The multipoles in MULT with nonzero ANGLE are defined by
Actually the summation is truncated at n + k <= 21 in the current version. While this defi
nition
converges to the regular one for multipoles when ANGLE -> 0, K0 and K1 of MULT are differe
nt from
those of BEND.
See also:
ANGLE
-
Relative phase offset. The stable synchrotron phase above the transition is near PHI
= 0.
The acceleration is given as
where ts is the equilibrium time determined by the valance between the acceleration and th
e radiation
loss around the ring.
-
Radius of the vacuum chamber. Effective when SPAC is ON.
See also:
SPAC
-
The skew 2-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 4-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 22-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 24-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 26-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 28-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 30-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 32-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 34-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 36-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 38-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 40-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 6-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 42-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 44-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 8-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 10-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 12-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 14-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 16-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 18-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
The skew 20-pole magnetic field component (times the length L).
where L is the length of the component. Positive sign means a horizontally focusing magnet
rotated
around z-axis by -90/(n+1) degree, i.e., ROTATE = (90/(n+1)) DEG .
See also:
L
-
Accelerating peak voltage in Volt.
where ts is the equilibrium time determined by the valance between the acceleration and th
e radiation
loss around the ring.
See also:
DVOLT
-
A octapole magnet.
-
If nonzero, the nonlinear Maxwellian fringe is suppressed.
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
The normal 8-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length.
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
-
A quadrupole magnet.
-
If nonzero, the nonlinear maxwellian fringe is suppressed. The effects of DISFRIN and
FRINGE are
summarized as
DISFRIN=0 DISFRIN<>0
Nonlinear Linear Nonlinear Linear
FRINGE=0 entr & exit none none none
FRINGE=1 entr entr none entr
FRINGE=2 exit exit none exit
FRINGE=3 entr & exit entr & exit none entr & exit
See also:
FRINGE
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
See also:
F2 FRINGE
-
See also:
F1 FRINGE
-
The effects of the linear fringe (characterized by F1 and F2), and the nonlinear Mexw
ellian fringe
are controled as:
DISFRIN=0 DISFRIN<>0
Nonlinear Linear Nonlinear Linear
FRINGE=0 entr & exit none none none
FRINGE=1 entr entr none entr
FRINGE=2 exit exit none exit
FRINGE=3 entr & exit entr & exit none entr & exit
See also:
F1 F2 DISFRIN
-
The normal 4-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length.
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
The transformation in a QUAD is a sequence of:
(nonlinear fringe at entrance)
canonical transformation by a generating function
G(x1, px2, y1, py2, p1) = H0(x1, px2, y1, py2, p1)
+ (D[H0, x1] D[H0, px2] + D[H0, y1] D[H0, py2])/2
where H0 = px2 dx1 + py2 dy1
dx1 = x1 (a/3 + b)
dy1 = -y1 (a + b/3)
a = K1 x1^2/p1/4
b = K1 y1^2/p1/4 .
(linear fringe at entrance)
px2 = exp(-a) px1
py2 = exp(a) py1
x2 = exp(a) x1 + b px1
y2 = exp(-a) y1 - b py1
z2 = z1 - (a x1 + b (1 + a/2) px2) px1
+ (a y1 + b (1 - a/2) py2) py1
where a = -K1 F1 abs(F1)/(24 p1 L)
b = K1 F2/L .
(body of quad)
The body is subdivided in n = 1 + floor(10 abs(K1 L)/EPS) (EPS = 1
is used when EPS = 0), then a transversely linear transformation
exp(:H:) is done in each slice with
H = ((-p + (px^2 + py^2)/(2 p) + E/v0) L + K1 (x^2 - y^2)/2)/n .
Between slices applied is the correction exp(:dH:) for the kinematical
term with
dH = (-sqrt(p^2 - px^2 -py^2) + p - (px^2 + py^2)/(2 p)) L/n .
In a solenoid, the forms of H and dH are modified.
(linear fringe at exit)
px2 = exp( a) px1
py2 = exp(-a) py1
x2 = exp(-a) x1 + b px1
y2 = exp( a) y1 - b py1
z2 = z1 + (a x1 - b (1 - a/2) px2) px1
- (a y1 - b (1 + a/2) py2) py1
where a = -K1 F1 abs(F1)/(24 p1 L)
b = K1 F2/L .
(nonlinear fringe at exit)
canonical transformation by a generating function
G(x1, px2, y1, py2, p1) = H0(x1, px2, y1, py2, p1)
+ (D[H0, x1] D[H0, px2] + D[H0, y1] D[H0, py2])/2
where H0 = px2 dx1 + py2 dy1
dx1 = x1 (a/3 + b)
dy1 = -y1 (a + b/3)
a = -K1 x1^2/p1/4
b = -K1 y1^2/p1/4 .
See also:
coordinates
-
A sextupole magnet.
-
If nonzero, the nonlinear Maxwellian fringe is suppressed.
-
If nonzero, the synchrotron radiation in the particle-tracking is inhibited.
See also:
RAD
-
Horizontal displacement of magnet. This applied before the rotation by ROTATE.
See also:
DY ROTATE DROTATE
-
Vertical displacement of magnet. This applied before the rotation by ROTATE.
See also:
DX ROTATE DROTATE
-
The normal 6-pole magnetic field component (times the length L).
where L is the effective length of the component. Positive sign means horizontal focusing.
See also:
L
-
The effective length.
-
Rotation in x-y plane. After displacing the magnet by DX and DY, rotate the magnet ar
ound the local
s-axis by -(amount given by ROTATE), then place the component. At the exit rotate back the
magnet
around the local s-axis at the exit, then take out displacement.
See also:
DX DY DROTATE
-
-
A solenoid. Unlike other elements, SOL elements inserted at boundaries or of a soleno
id or at where
the field changes. Between SOL elements DRIFT, BEND(straight bend only), QUAD, and MULT el
ements
can be inserted. The longitudinal field of the solenoid overlaps on those elements.
In a SOL region, the coordinate is shifted on the axis of the solenoid, no matter how t
he design
orbit bends there. The x-direction of the coordinate in a solenoid is so chosen as to CHI3
= 0. At
the exit of a solenoid, the coordinate is shifted back to the design orbit, but the value
of CHI3
is so determined as to set CHI3 zero at the nearest MARK element which has GEO = 1 after t
he exit.
The offset and orientation of the design orbit can be given by keywords DX, DY, DPX, DPY a
t a SOL
element with GEO = 1. SOL can be used to shift the coordinate to the actual orbit even wit
hout BZ.
It is useful to define the coordinate with magnets with DX and DY.
See also:
geometric-functions MARK
-
BOUND = 1 must be given at both sides of the boundaries of a solenoid, otherwise SOL
only specifies
the change of BZ
-
The longitudinal field of a solenoid. If a SOL is used with BOUND = 0 (default), only
BZ is used
to change the field, and no coordinate transformation is applied.
-
Disables the nonlinear fringe of solenoid if nonzero. The default is 0. The transform
ation for the
nonlinear fringe is expressed by
exp(:H:) ,
H = -Bz/(8 Brho p^2) p_phi p_r,
where
p_phi = x py - y px ,
p_r = x px + y py ,
whose canonical partners are
phi = ArcTan[y/x] ,
r = Log[x^2 + y^2]/2 ,
respectively.
-
An offset of the design ORBIT angle CHI1 relative to the solenoid axis at SOL with GE
O = 1.
See also:
GEO DX DY DPY CHI1
-
An offset of the design ORBIT angle CHI2 relative to the solenoid axis at SOL with GE
O = 1.
See also:
GEO DX DY DPX CHI2
-
An x-offset of the design ORBIT relative to the solenoid center at SOL with GEO = 1.
See also:
GEO DY DPX DPY
-
A y-offset of the design ORBIT relative to the solenoid center at SOL with GEO = 1.
See also:
GEO DX DPX DPY
-
The length of fringe of the solenoid field. It affects only the EMITTANCE calculation
. If F1 = 0
(default), no radiation arises at the fringe.
-
One of boundaries (with GEO = 1) of a solenoid must have GEO = 1 to specify the align
ment of the
design orbit. At a SOL element with GEO = 1, the design orbit is determined by DX, DY, DPX
, DPY parameters
See also:
DX DY DPX DPY
An expression in FFS consists of a symbol, constants, and operators.
>>> A symbol is a characters of any length starting with an alphabet or $.
>>> There are two kinds of constants, real number and character-string.
real number is a number in fortran-line format.
character-string is a set of characters surrounded by "" or ''.
special-characters can be specified with backslash.
>>> Available operators are (in the order of the priority):
#,##,
?,
::,
@,
[],
++, --,
/@, //@, @@,
.,
^,
*, /,
+, -,
==, <>, >, <, >=, =>, <=, =<,
===, <=>,
~,
&&,
||,
.., ...,
|,
:,
->, :>,
/., //.,
+=, -=, *=, /=,
&,
//,
/:,
=, :=, ^=, ^:=, =.
;,
{}
An operator with higher priority is operated first. An expression enclosed in () is evalua
ted first.
Most mathematical operations are threaded into a list, i.e., {a,b} + {c,d} gives {a + b,c
+ d}, etc.
Each operators can be used as a function using its name. For example, Plus[x,y] gives th
e same
result as x + y.
See also:
constants functions command-syntax character-string
-
operator for subtraction or unary minus.
-
operator for division.
-
a+=b is equivalent to a=a+b .
-
a | b | ... represents a pattern which matches one of patterns a, b, ...
-
a && b returns True(==1) when both a and b are nonzero real, False(==0) otherwise.
b is not evaluated
when a is zero.
-
f@@a applies function f to subexpressions of a. f@@[a,level] specifies a levelspec to
apply by level.
See also:
Apply
-
a ; b evaluates a, then evaluates b and returns its result.
-
a-- decrements a by 1, returning the old value of a. --a decrements a by 1, returning
the new value
of a.
-
a/=b is equivalent to a=a/b.
-
a . b returns the inner product of a and b.
-
a == b returns True(==1) if a and b have the same type and the same value. It returns
False(==0)
if a and b have the same type but the different values. Otherwise returns the expression a
== b.
-
a & is a pure-function whose argument is specified #, #n, ##, ##n.
See also:
Slot(#) SlotSequence(##) functions Function(&)
-
If both a and b are real, a > b returns True if a is greater than b, False otherwise.
It causes an
error when a or b is not real.
-
If both a and b are real, a => b returns True if a is greater than or equal to b, Fal
se otherwise.
It causes an error when a or b is not real.
-
a++ increments a by 1, returning the old value of a. ++a increments a by 1, returning
the new value
of a.
-
If both a and b are real, a < b returns True if a is less than b, False otherwise. It
causes an error
when a or b is not real.
-
If both a and b are real, a <= b returns True if a is less than or equal to b, False
otherwise. It
causes an error when a or b is not real.
-
{a,b,c...} is a list structure.
-
f/@a maps function f to subexpressions of a. f/@[a,level] specifies a levelspec of ma
p by level.
See also:
Map
-
f//@a maps function f to all subexpressions of a. f//@[a,Heads->True] maps including
the heads of
a and its subexpressions.
-
f@a refers the member a of an instance or a class f. Otherwise it is same as f[a]. f@
g@h means (f@g)@h,
and f@g[h] (f@g)[h].
-
symbol::tag returns a message associated with symbol and tag
symbol::tag = message sets a message identified by symbol
-
~a returns True(==1) when a is zero, False(==0) when a is a nonzero real.
-
a || b returns True(==1) when a is nonzero real or b is nonzero real, False(==0) othe
rwise. b is
not evaluated when a is nonzero.
-
a[[b,..]] is a subexpression of an expression a.
If an index is omitted or Null as a[[,b]], Part returns a list of elements whose correspo
nding index
takes the entire range. For instance,
{{1, 2}, {3, 4}, {5, 6}}[[,2]] gives {2, 4, 6}.
See also:
Part
-
pattern?test matches to an object which matches pattern then test[object] gives True.
-
a + b returns the sum of a and b.
-
a ^ b returns the power of a to b.
-
p.. matches sequence of one ore more expressions, each matching p.
-
p... matches sequence of zero ore more expressions, each matching p.
-
expr/.rule replaces all subexpressions of expr using rule.
-
expr//.rule replaces all subexpressionso of expr using rule, while a replacement is p
erformed.
-
pattern->expr represents a rule for ReplaceAll.
-
pattern:>expr represents a rule for ReplaceAll, where expr is kept unevaluated until
the replacement.
See also:
Literal
-
a === b returns True(==1) if a and b have the same type and same value, False(==0) ot
herwise.
-
a[b,c,..] means a list of b, c,.. with the head a. It is evaluated as a function-refe
rence when a
is a function or a defined-function. When a is a list with head List, it is interpreted as
a part
specification of a list. When a is a character-string, it is interpreted as a substring sp
ecification.
When a is an operator, it is an expression b (a) c (a) .. . When a is Null, it means a seq
uence.
-
a = value sets the value b to the symbol a. {a,b,..}={v1,v2,..} sets a,b,c simultaneo
usly. a[b,c,..]=v1
sets the part of a[b,c,..] if a is a list. a[b,c,..] = expression defines the value a[b,c,
..] if
a is not a list.
-
same as Set but the right hand side is not evaluated when it is set.
See also:
Set(=)
-
a // b converts a and b to character-strings, then join them.
See also:
StringJoin
-
a-=b is equivalent to a=a-b .
-
symb/:lhs = rhs sets rhs to lhs, associated with symbol symb. symb/:lhs := rhs sets r
hs to lhs unevaluated,
associated with symbol symb. symb/:lhs =. unsets lhs, associated with symbol symb.
-
a * b returns the product of a and b.
-
a*=b is equivalent to a=a*b .
-
a <> b returns True(==1) if a and b have the same type but the different values. It r
eturns False(==0)
if a and b have the same type but the same value. Otherwise returns the expression a <> b.
-
a <=> b returns True(==1) if a and b have the different types or different values. Fa
lse(==0) otherwise.
-
a=. clears the definition assigned to a.
See also:
Clear
Usage: IF expr1 body1 [ELSEIF expr2 body2 [ELSEIF ..]] [ELSE body3] ENDIF
This is a FORTRAN77 like IF-structure. If the expression expr1 is True(==1) or nonzero, ex
ecutes
commands in body1. If it is False(==0), skip commands until ELSE, ELSEIF or ENDIF appears
at the
same level of the IF-structure, and executes commands after ELSE or ENDIF, or executes the
ELSEIF
command. If expr1 is not a real number, an error message is printed and ignores the comman
d line.
See also:
If ELSEIF ENDIF
Usage: IF expr1 body1 [ELSEIF expr2 body2 [ELSEIF ..]] [ELSE body3] ENDIF
This is a FORTRAN77 like IF-structure. If the expression expr1 is True(==1) or nonzero, ex
ecutes
commands in body1. If it is False(==0), skip commands until ELSE, ELSEIF or ENDIF appears
at the
same level of the IF-structure, and executes commands after ELSE or ENDIF, or executes the
ELSEIF
command. If expr1 is not a real number, an error message is printed and ignores the comman
d line.
See also:
IF ELSE ENDIF
Usage: (1) EMIT
(2) EMIT dp
(1) EMIT calculates the closed orbit, the normal coordinate, and the equilibrium emittance
assuming the current beam line is a positron ring. One of EMITTANCE(EMIT), the Emittance[
] function, or the EMIT command in the MAIN level are necessary to be done in prior to mul
ti-turn tracking. See multi-turn-tracking.
(2) EMIT dp, where dp is |df_rf/f_rf|/(alpha_p == momentum compaction), does EMIT for five
rf frequencies:
then prints out a table of the dependences of various quantities on the frequency shift.
The results of EMITTANCE(EMIT) are affected by flags COD, RADCOD, RFSW, INTRA, WSPAC, E
MIOUT,
CODPLOT and special-variables MOMENTUM, CHARGE, FSHIFT, MINCOUP, PBUNCH. The flag TRPT or
RING affects
only Emittance[], as EMITTANCE(EMIT) automatically set RING.
EMITTANCE(EMIT) returns the equilibrium emittances in variables EMITX, EMITY, EMITZ, an
d the equilibrium
bunch length in SIGZ, the relative momentum spread in SIGE, and the longitudinal equilibri
um position
DTSYNCH.
The map used in EMIT is slightly different from that used in the tracking. For instance
, the edge
angle of a bend is approximated by a thin quad. If the edge angle is large and the curvatu
re is small,
EMIT may give a wrong answer. This will be corrected in near future.
See also:
multi-turn-tracking extended-Twiss-parameters COD RADCOD RFSW INTRA EMIOUT WSPAC CODPLOT
TRPT MOMENTUM CHARGE FSHIFT MINCOUP PBUNCH EMITX EMITY EMITZ SIGE SIGZ DTSYNCH
Emittance
Closes the current output-stream and set the output stream to the standard output(6).
It also suspends
all the input streams and switches to the standard input(5). Since this command affects al
l input
and output streams, you may consider to use TERMINATE(TERM) or CLOSE(CLO) to suspend or cl
ose them
selectively.
See also:
TERMINATE(TERM) CLOSE(CLO) INPUT(IN) READ OUTPUT(OUT) APPEND(APP)
Usage: IF expr1 body1 [ELSEIF expr2 body2 [ELSEIF ..]] [ELSE body3] ENDIF
This is a FORTRAN77 like IF-structure. If the expression expr1 is True(==1) or nonzero, ex
ecutes
commands in body1. If it is False(==0), skip commands until ELSE, ELSEIF or ENDIF appears
at the
same level of the IF-structure, and executes commands after ELSE or ENDIF, or executes the
ELSEIF
command. If expr1 is not a real number, an error message is printed and ignores the comman
d line.
See also:
IF ELSE ELSEIF
Usage: EXEC character-string-expression
executes the character-string-expression as FFS commands.
See also:
expression FFS ToExpression
EXPAND distributes all variable keys to each corresponding components. Individual de
viations (machine
errors) are cleared.
See also:
GO CALCULATE(CAL) EMITTANCE(EMIT)
Usage: [NO]flag
turns the flag on. If NO is prepended to flag, the flag is turned off. Some flags have ant
onym which
works in the opposite way. Flags can be accessed in the function-syntax with the form ?fla
g, which
returns True (=1) when the flag is on, or False (=0) otherwise. Some flags can be accessed
by the
ON/OFF commands at the MAIN level.
Status of all flags are displayed by the STATUS(STAT) command.
See also:
STATUS(STAT) PatternTest(?)
-
ABSW or NORELW sets the weights of variable elements independent from their values in
the matching.
Otherwise they are weighted relatively.
See also:
RELW
-
BIPOL or NOUNIPOL allows the change of sign of the value of the element during the ma
tching. It affects
the default keywords of all elements. This is overridden by MIN, MAX specification or Vari
ableRange
of each element.
See also:
UNIPOL default-keyword set-value-of-element VariableRange
-
If CALC4D is on, the optics calculation in CAL and GO performs a 4x5 calculation (4D
+ dispersion).
The antonyms is CALC6D. The Default is CALC4D.
See also:
CALC6D CALCULATE(CAL) GO
-
If CALC6D is on, the optics calculation in CAL and GO performs full 6D calculation, w
hich may takes
RADCOD into account. The antonyms is CALC4D. The Default is CALC4D.
See also:
CALC4D CALCULATE(CAL) GO
-
CELL or NOINS sets the periodic condition in calculating the optical-functions.
See also:
INS CALCULATE(CAL) GO optical-functions matching-function-commands
-
CMPLOT enables the shift of the center of mass at the beginning of the tracking. This
is almost obsolete.
-
COD turns on finding the closed-orbit in the emittance calculation. Accessible in MAI
N level.
See also:
EMITTANCE(EMIT)
-
CODPLOT lets the emittance calculation return the information on the closed-orbit, ex
tended Twiss
parameters, and the beam size along the beam line into the FFS optics buffer, which can be
shown
by DISPLAY(DISP) or DRAW commands as well as Twiss and OpticsPlot functions.
See also:
EMITTANCE(EMIT) DISPLAY(DISP) DRAW WSPAC RADTAPER
-
CONV is a flag set by the CALCULATE(CAL) or GO commands. It becomes True when Matchin
gResidual is
less than CONVERGENCE.
See also:
CALCULATE(CAL) GO MatchingResidual CONVERGENCE
-
When CONVCASE is on, FFS command line parser converts the input characters to the upp
er case.(Default
on) CONVCASE actions for the element names and patterns CAN be overridden by PRSVCASE flag
.
See also:
PRSVCASE
-
DAMPONLY is the antonym of FLUC.
See also:
FLUC
-
DAPERT enables the DAPERT procedure in the multi-turn tracking to obtain the dynamic
aperture diagram.
Accessible in the MAIN level.
See also:
functions DynamicApertureSurvey
-
In the case of CELL, if the total tune deviates across a difference resonance, it is
counted as unstable.
The default is NODIFFRES.
See also:
INTRES HALFRES SUMRES STABLE
-
ECHO enables the echo of the main input in the MAIN level.
-
EMIOUT turns on the extended output of emittance calculation.
Accessible in the MAIN level.
See also:
EMITTANCE(EMIT)
-
When FFSPRMPT is off(default) the input prompt is In[n]:= , where n is $Line+1. Other
wise the prompt
is the traditional FFS prompt, showing the FIT location and the DISP range.
See also:
$Line LOG
-
FIXSEED or NOMOVESEED disables the change of the seed of the random number generator
after the particle
tracking.
See also:
MOVESEED MEASURE(MEA) SEED
-
FLUC or NODAMPONLY enables the diffusion due to synchrotron radiation in the particle
tracking. Otherwise
only the damping is enabled when RAD is ON.
See also:
DAMPONLY RAD RADCOD
-
GAUSS or NOUNIFORM sets the momentum distribution of the incoming beam to be Gaussian
, otherwise
uniform(square) distribution is assumed. It affects the beam size calculated by Twiss para
meters.
See also:
UNIFORM MEASURE(MEA) BEAM(B) special-variables DP
-
When GEOCAL is on(default), the geometry of the beam line is always updated by CALCUL
ATE(CAL) or
GO commands using the current values of components. The coordinate transformation by SOL i
s also
updated. When GEOCAL is off, the geometry is never updated. It is useful to simulate misal
ignments
within a solenoid, etc.
See also:
GEOFIX CALCULATE(CAL) GO SOL
-
GEOFIX is the antonym of GEOCAL.
See also:
GEOCAL
-
In the case of CELL, if the total tune deviates across a half-integer resonance, or t
he traces is
less than -2, it is counted as unstable (~?STABLE). Otherwise the optics is recognized as
STABLE.
The default is HALFRES.
See also:
INTRES SUMRES DIFFRES STABLE
-
IDEAL or NOREAL inhibits to use the component-specific deviations (i.e., machine-err
ors) in the
optics calculation.
See also:
REAL CALCULATE(CAL) GO machine-errors
-
INS is the antonym of CELL.
See also:
CELL
-
INTRA turns on the calculation of intra-beam scattering in the emittance calculation.
Accessible
in MAIN level.
See also:
EMITTANCE(EMIT)
-
In the case of CELL, if the total tune deviates across an integer resonance, or the t
race is larger
than 2, it is counted as unstable (~?STABLE). Otherwise the optics is recognized as STABLE
. The default
is INTRES.
See also:
HALFRES SUMRES DIFFRES STABLE
-
JITTER or NOQUIET allows jitter of the center-of-mass of the incoming beam in the cas
e of TRPT. Otherwise
the center-of-mass statistically fluctuates depending on the number of particles.
See also:
QUIET MEASURE(MEA) TRPT
-
LOG enables the echo of all inputs in the MAIN level. Also suppresses the prompt in FFS.
See also:
ECHO
-
LWAKE turns on optics calculation with Longitudinal WakeFunction
See also:
WakeFunction TrackParticles InitialOrbits TWAKE
-
MOVESEED is the antonym of FIXSEED.
See also:
FIXSEED
-
When PHOTONS is ON (default is OFF), TrackParticles generates a list of all photons r
adiated through
the tracking. The list is assigned to a symbol PhotonList.
See also:
PhotonList TrackParticles
-
POL turns on spin tracking and the calculation of equilibrium polarization in EMIT/Em
ittance[].
See also:
RADPOL EMITTANCE(EMIT) Emittance TrackParticles
-
When PRSVCASE is on, FFS command line parser preserves the input characters for the e
lement names
and patterns.(Default off)
See also:
CONVCASE
-
When on, performs space-charge simulation in a "Particle-In-Cell" method. PSPAC is ef
fective in tracking
only.
Do not confuse PSPAC with SPAC/WSPAC.
See also:
PSPACNX PSPACNY PSPACNZ PSPACDX PSPACDY PSPACDZ
-
QUIET is the antonym of JITEER.
See also:
JITTER
-
RAD turns on the synchrotron radiation in the particle-tracking. Accessible in the MA
IN level.
See also:
RADCOD FLUC
-
RADCOD turns on the energy loss due to synchrotron radiation at the closed-orbit in t
he emittance
calculation. Also turns off the implicit acceleration in the tracking to compensate the en
ergy loss
automatically, in the case that TRPT is ON. Accessible in MAIN level.
See also:
RAD FLUC TRPT
-
When RADLIGHT is on, the function TrackParticles returns a list of trajectories which
are used to
calculate the synchrotron radiation field.
See also:
TrackParticles RadiationField RadiationSpectrum
-
If POL is on, RADPOL turns on Sokolov-Ternov effect in tracking.
See also:
POL
-
Scales all magnets except for solenoids according to the local momentum (DDP) of the
closed orbit.
It uses the average of DDPs at the entrance and the exit. For tracking, RADCOD and ( CAL/G
O with
CALC6D or EMIT(Emittance[]) ) is necessary. CAL/GO with CALC4D will clear the necessary in
formation
for tracking with RADTAPER.
RADTAPER sets the momentum deviation of the closed orbit to DP0, which is an arbitrary ch
oice of
an under-deterministic problem of tapering. Thus the difference in the path length around
the ring
is adjusted by automatically updating FSHIFT.
See also:
RADCOD CALC6D CALC4D EMITTANCE(EMIT) CALCULATE(CAL) GO DP0 FSHIFT
-
REAL is the antonym of IDEAL.
See also:
IDEAL
-
RELW is the antonym of ABSW.
See also:
ABSW
-
RFSW turns on the acceleration by CAVI and TCAVI element in the particle-tracking and
the emittance
calculation. Accessible in MAIN level, but FFS always turns RFSW on at the beginning of th
e session.
-
RING is the antonym of TRPT.
See also:
TRPT
-
When on with WSPAC, in tracking, the space charge force is calculated relative to the
center of mass
of the current set of particles each time. Otherwise(default) it is calculated relative to
the closed
orbit given by EMIT. SELFCOD is useful when the closed orbits given by EMIT and TRACK are
different.
See also:
WSPAC
-
SORG sets the origin of S (design orbit length) at the location set by ORG.
See also:
ORG
-
When SPAC is on, tracking is done with space charge effect. The actual number of part
icles in the
beam and the number of macro particles are given by PBUNCH and NP, respectively. This calc
ulation
assumes a cylindrical symmetry of the chamber whose radius is given by RADIUS of DRIFT and
MULT elements.
If RADIUS is positive, an aperture is also set at RADIUS to make particle loss. If RADIUS
is zero,
no space charge calculation is done. If RADIUS is negative, no space charge effect is take
n, but
the aperture is set at -RADIUS.
Do not confuse SPAC with WSPAC.
See also:
NP PBUNCH WSPAC
-
STABLE is a flag set by the CALCULATE(CAL) or GO commands in the case of CELL. It bec
omes True when
the closed orbit is found and the optics is stable in both x and y.
See also:
CALCULATE(CAL) GO INTRES HALFRES SUMRES DIFFRES
-
In the case of CELL, if the total tune deviates across a sum resonance, it is counted
as unstable.
The default is SUMRES.
See also:
INTRES HALFRES DIFFRES STABLE
-
TRPT or NORING declares that the beam line is a transport line, not a part of a stora
ge ring. The
nominal momentum be changed in the beam line due to acceleration. The default momentum dis
tribution
becomes uniform distribution. The default is RING or NOTRPT. TRPT affects Emittance[] to i
gnore equilibrium
calculation for a transport line.
See also:
DISPLAY(DISP) RING UNIFORM GAUSS
-
TWAKE turns on optics calculation with Transverse WakeFunction
See also:
WakeFunction TrackParticles InitialOrbits LWAKE
-
UNIFORM is the antonym of GAUSS. It assumes the momentum distribution to be a uniform
(square) within
+-DP.
See also:
GAUSS TRPT
-
UNIPOL is the antonym of BIPOL.
See also:
BIPOL
-
UNSTABLE is the antonym of STABLE.
See also:
STABLE
-
When on, performs space-charge simulation in a "strong-weak" mode. The beam size thro
ugh the beam
line is to be calculated by EMIT with CODPLOT. The space-charge force is calculated assumi
ng Gaussian
distribution in all dimensions, and particles/bunch given by PBUNCH. WSPAC is effective in
optics
and emittance calculations and tracking.
Do not confuse WSPAC with SPAC.
See also:
EMITTANCE(EMIT) PBUNCH CODPLOT MINCOUP SELFCOD SPAC
FFS functions:
Constants:
Degree GoldenRatio I INF* Infinity NaN* Pi SpeedOfLight
Elementary-functions:
ArcCos ArcCosh ArcSin ArcSinh ArcTan ArcTanh Cos Cosh Exp Log Sin Sinh
Sqrt Tan Tanh
Special-functions:
BesselI BesselJ BesselK BesselY BesselJZero Erf Erfc Factorial
Gamma LogGamma LogGamma1 GammaRegularized GammaRegularizedQ*
GammaRegularizedP* GaussianCoulomb* GaussianCoulombU*
GaussianCoulombFitted* LegendreP*
Numerical-functions:
Abs Ceiling Floor Max Min MinMax* Mod Negative NonNegative Positive
Round Sign FractionalPart
Matrix-operations:
Det Eigensystem IdentityMatrix Inner LinearSolve Outer SingularValues*
Transpose
Random-number:
GaussRandom* Random* SeedRandom
Complex:
Arg Complex ComplexQ Conjugate Im Re
Rational:
Rational FromRational ContinuedFraction FromContinuedFraction SmallPrime
Numerator Denominator
Fourier-Transformation:
Fourier InverseFourier
Data-Manipulation:
FindRoot Fit* NIntegrate* PolynomialFit* Spline*
Calculus:
D NIntegrate
Minimization:
DownhillSimplex*
List-manipulations:
Append Complement Delete Depth Difference* Dimensions Drop Extract Flatten
FlattenAt HeldPart Insert Intersection Join Length Part Partition Prepend
Product Range ReplacePart Rest Reverse RotateLeft RotateRight Select
Sort Sum Take Table Union
Character-strings:
FromCharacterCode CharacterPosition Characters DigitQ LetterQ StringDrop
StringFill* StringInsert StringLength StringPosition StringTrim*
Symbol SymbolName ToCharacterCode ToLowerCase ToUpperCase ToExpression
Functional-Operations:
Apply Cases Count DeleteCases Identity FixedPoint* FixedPointList*
Fold Function Level Map MapAll MapAt MapIndexed MapThread Nest Position
Replace Scan ScanThread* SelectCases* SwitchCases* Thread
Object-oriented programing and context:
Begin BeginPackage Class* End EndPackage
Flow-Control:
Break Catch Check Continue Do For Goto If Label Return Switch Throw Which
While
Tests:
AtomQ ComplexQ DirectoryQ* EvenQ FileQ* MatchQ MatrixQ MemberQ NearlySameQ*
Negative NonNegative NumberQ OddQ Order Positive RealQ StringQ* VectorQ
BoundQ* FBoundQ*
Input/Output:
Close Flush* Get OpenRead OpenWrite OpenAppend Print Put Read ReadString SeekFile*
Short* StringToStream Write WriteString
File System:
CopyDirectory CopyFile CreateDirectory DeleteDirectory DeleteFile
DirectoryName FileByteCount FileDate FileNames FileType
RenameDirectory RenameFile SetFileDate ToFileName
Scoping:
Block Module With*
Attributes:
Attributes* Clear Evaluate Head Hold Literal Protect ReleaseHold
SetAttributes* Unevaluated Unprotect
GUI Widget:
Window* PanedWindow* Frame* LabelFrame* Canvas* TextLabel* TextMessage*
Button* CheckButton* RadioButton* Menu* OptionMenu* MenuButton*
Entry* SpinBox* ListBox* ScrollBar* Scale* TextEditor*
Graphics:
BeamPlot* ColumnPlot* HistoPlot* ListContourPlot ListDensityPlot
ListPlot Plot Show FitPlot* GeometryPlot* OpticsPlot* TkPhotoPutBlock*
System Interface:
Directory Environment GetEnv* GetGID* GetPID* GetUID* ProcessStatus*
SetDirectory SetEnv* System* TemporaryName* MkSecureTemp* RealPath*
Multiprocessing:
BiPipe* Fork* OpenShared* Shared* Wait*
Utilities:
Date DateString* Definition* FromDate* ToDate ToDateString* Pause
MemoryCheck* Message Off On Sleep TimeUsed Timing TracePrint
Functions listed above work basically in the same way as Mathematica's
except those marked by *.
FFS-dedicated-functions:
BeamMatrix CalculateOptics DynamicApertureSurvey Element Emittance FFS
FitValue FitWeight GeoBase LINE OptimizeOptics OrbitGeo RadiationField
RadiationSpectrum SymplecticJ SetElement TrackParticles Twiss VariableRange
SynchroBetaEmittance TouschekLifetime WakeFunction
Beam-line-functions:
BeamLine BeamLineName ExtractBeamLine PrintBeamLine WriteBeamLine
See also:
expression constants physical-constants beam-line-functions
-
-
Usage: Fit[data, expr, var,
{par1, ini1, [{min1, max1}] }, .. ,{parn, inin, [{minn, maxn}]},
[options..] ]
performs a nonlinear fitting of data with an expression expr.
data: list of {xi,yi}, {xi,yi,dyi}, or {xi,yi,dxi,dyi}, where dxi and dyi
are the standard deviation of the i-th point.
expr: an expression containing var as the x-variable, and
parameters par1,..,parn explicitly. Use Evaluate[fun] if an implicit
expression is necessary.
var: a symbol to express the x-axis variable.
par: parameter symbol to be varied in the fitting.
ini: initial value of the parameter. It must be specified.
(min, max}: optional range of parameter.
Fit returns the result as a list:
{par1 -> v1, .., parn->vn, ChiSquare -> chisq, GoodnessOfFit -> good,
ConfidenceInterval -> {c1, .., cn}, ConvarianceMatrix -> cov},
where v1,..,vn are the values of the parameters which minimizes chi-square, chisq is the r
esulting
minimum value of the total chi-square (when no error is given for yi, variance is returned
), good
is a number given by GammaRegularized[(ndata-npara)/2,chisq/2] to represent the goodness o
f the fit,
c1, .., cn are the estimated errors in parameters, and cov is the covariance matrix. A typ
ical criterion
of the goodness is (good > 0.1).
Options are
MaxIterations Maximum number of iterations.
D If True (default), tries to use analytical derivative.
Cutoff If nonzero, set the saturation point for each data as:
chi-suare = Sum_i ( Min[Cutoff, Max[-Cutoff, (d_i - f_ i) / sigma_i]]^2 ) ,
which is a sort of robust M-Estimates. By Cutoff, the fit
tends to ignore tail data which are beyond Cutoff.
If Cutoff is zero (default), it is ignored.
See also:
FitPlot
-
Obtain the emittance, beta, alpha, etc. from data of particles x and px using FitGaus
sian.
FitEmit[x, px] ,
where x and px are the lists of data of the particles in the phase space, returns a list
{{xmean, pxmean, alpha, beta, emittance},
{xmean, pxmean, alpha, beta, emittance}_conf},
where the second component is the confidence intervals of the results.
See also:
FitGaussian
-
Performs Gaussian fit of 1D list data:
FitGaussian[data, [opt, ...]]
returns a list
{sigma, mean, {sigma_conf, mean_conf}, chisq} ,
where sigma_conf and mean_conf are the confidence interval of the results sigma and mean,
respectively.
The arguments opt... are options for Fit. If Plot -> True is specified as the option, a pl
ot of the
fitting will be made.
See also:
Fit FitEmit
-
NIntegrate returns numerical integration of a Real or Complex
function
Usage: NIntegrate[f, {x, x0, x1}, options]
where f is a function containing Symbol x as the independent variable. The integral range
is from
x0 and x1. The function f must contain the symbol x explicitly.
Options Default Description
-------------------------------------------------------------
AccuracyGoal 1e-13 Relative accuracy
InitialPoints 20 Number of initial points where
the function is evaluated.
-
Usage: PolynomialFit[data, n]
performs a 1D linear regression of data.
data: list of {xi,yi}
n: the order of the polynomial
Fit returns the result as a list:
{{c0, .., cn}, {Residual -> res}} ,
where c0 .. cn are the coefficients of the fitted polynomial, y = c0 + c1 x + .. + cn x^n
. Res is
the rms residual of the fit.
See also:
FitPlot
-
Spline returns data for cubic-spline interpolation.
Usage: sp = Spline[list, [Derivative->{dy1,dy2}] ]
where list contains data in the form as {{x1,y1}, ..} or {{x1,{y11, y12, ..}}, ..}.
Complex number can be allowed for y, but not for x.
This spline assumes y''=0 at the boundary, unless Derivative->{dy1,dy2} is specified to c
onstrain
the derivative at each end to dy1 or dy2. They can be Null to unspecify the constraint at
one of
the boundary. The resulting data of the spline is assigned sp as a SplineData object. Then
one can
calculate the interpolated data by
sp[x] value of y at x.
Derivative[1][sp][x] value of y' at x.
Derivative[2][sp][x] value of y'' at x.
Integrate[sp[x],{x, x0, x1}] integral of sp[x] from x0 to x1.
Example:
sp=Spline[{{1,2},{3,5},{4,2},{5,7}}];
Plot[{sp[x],Derivative[1][sp][x],Derivative[2][sp][x],Integrate[sp[y],{y,1,#}]&[x]}, {x
,1,5},
FrameLabel->{"x"}, Thickness->2, Legend->{"sp[x]","sp'[x]","sp''[x]","Int sp[x]"}];
Update[];
See also:
defining-functions Plot NIntegrate
-
Usage: DownhillSimplex[initial, f, options]
minimizes a function f by the downhill simplex method, starting from an initial simplex in
itial.
Suppose f is a function of n variables. Then initial is a list of n+1 elements, each o
f which
is a list of the form
{f[vi], vi} ,
where vi is a list of n values corresponding to each variable. The initial must be sorted
in ascending
order of f, i.e.,
initial=Sort[Map[{f[#],#}&,vlist]]
generates initial from a list of variables vlist.
DownhillSimplex returns the final simplex in the same form as initial.
Options:
VariableRange -> {{min1 .. minn}, {max1 .. maxn}} gives the range of n
variables. The default is -Infinity to Infinity for all variables.
MaxIteration -> maxi gives the limit of number of iterations. The
default is Max[100, 10*(n+1)].
Output -> lfn sets the output file number for the intermediate results.
the default is 6 (stdout).
Tolerance -> tol sets the tolerance to judge the local minimum.
If (fmax-fmin)/(abs(fmax)+abs(fmin)) becomes less than tol, the
iteration loop terminates. The default is 10^-6.
Examples:
f:=Apply[Function[{x,y},((x^2+y^2)-1)*(x^2+y^2)-(x-.5)/3.],#]&;
v={{1.,1.},{0.,-1.},{0.,1.}};
limit={{-0.5,-1.5},{0.65,1.5}};
p=Sort[Map[{f[#],#}&,v]]
DownhillSimplex[p,f,MaxIteration->100,
Tolerance->1e-4,VariableRange->limit]
See also:
FFS-dedicated-functions:OptimizeOptics
-
-
Apply[f, x [, level]] or f@@x [f@@[x, level]]
takes the bod of a list x as the argument sequence of f, and returns the result:
f@@{a, b, c} ===> f[a, b, c]
An optional argument specifies the level-spec.
See also:
Apply (@@) Map Scan MapThread level-spec
-
Cases[l, pat [, level [,n]]]
returns a list of parts of l, which match a pattern pat. Optional level-spec l and the max
imum number
of results n can be specified.
See also:
level-spec pattern Position Deletecases
-
DeleteCases[l, pat [, level [,n]]]
returns a list of parts of l, which do not match a pattern pat. Optional level-spec l and
the maximum
number of results n can be specified.
See also:
level-spec pattern Cases Position
-
Difference[list] returns Rest[list] - Drop[list, -1] .
-
FixedPoint[f, e] starts from f[e] then applies f repeatedly until the result no longe
r changes. FixedPoint[f,
e, n] specifies the maximum number of iterations by n. An option SameTest->s specifies the
test function.
Threshold->re, and AbsoluteThreshold->ae set the relative and absolute accuracy, respectiv
ely, when
SameTest->NearlySameQ (default).
See also:
FixedPointList
-
FixedPointList[f, e] returns the intermediate values of FixedPoint[f, e] as a list. F
ixedPointList[f,
e, n] and options for FixedPoint are valid.
See also:
FixedPoint
-
Functions Map, Apply, Scan, Cases, Position, Count, Level, DeleteCases takes an optio
nal argument
level to specify which level to operate:
value operates
n_Real from level 1 through level n
{n_Real} only on level n
{n1_Real, n2_Real} from leveln1 through level n2
If n is negative, it counts from the deepest level of each element.
Examples: f@@[{{a, b}, {c, d}}, {1}] ===> {f[a, b], f[c, d]}
See also:
Map Apply Scan Cases Position Count Level DeleteCases
-
Map[f, x [, level]] or f/@x [f/@[x, level]]
operates f over each element of a list x and returns the result as a list:
f/@{a, b, c} ===> {f[a], f[b], f[c]}
An optional argument specifies the level-spec.
See also:
@/ Scan Apply MapThread level-spec
-
MapThread[f, l] ===> f@@[Thread[l], {1}]
Example: MapThread[f, {{1, 2}, {3, 4}}] ===> {f[1, 3], f[1, 4]}
See also:
ScanThread Thread Map Apply
-
Position[l, pat [, level [,n]]]
returns a list of indices of parts of l, which match a pattern pat. Optional level-spec l
and the
maximum number of results n can be specified.
See also:
level-spec pattern Cases DeleteCases
-
Scan[f, x [, level]]
operates f over each element of a list without returning the result:
Scan[f, {a, b, c}] ===> {f[a], f[b], f[c]};Null
An optional argument specifies the level-spec.
See also:
Map Apply MapThread level-spec
-
ScanThread[f, l] ===> (f@@[Thread[l], {1}];Null) ,
which is equivalent to MapThread without returning the results.
See also:
MapThread Thread Map Apply
-
Usage: SelectCases[list, {test1,..}]
returns a list {list1, .. }, where list1 is a list of subexpressions which makes test1 Tru
e, etc.
If the second argument is like {c1, .. , True&}, the last of the returned list contains s
ubexpressions
which make none of c1, ... True.
See also:
SwitchCases
-
Usage: SwitchCases[list, {case1,..}]
returns a list {list1, .. }, where list1 is a list of subexpressions which match case1, et
c. SwitchCases
does what are done by Cases and DeleteCases simultaneously. If the second argument is like
{c1, ..
, _}, the last of the returned list contains subexpressions which match none of c1, ...
See also:
SelectCases
-
Thread[l] returns a threaded list of l:
Thread[{{1, 2}, {3, 4}}] ===> {{1, 3}, {2, 4}}
Thread[{{1, 2}, {3, 4}, 5}] ===> {{1, 3, 5}, {2, 4, 5}}
If an optional second argument h is given, Thread operates only over on a structure whose
head is
h:
Thread[{{1, 2}, {3, 4}} , f] ===> {{1, 2}, {3, 4}}
Thread[{f[1, 2], f[3, 4]} , f] ===> f[{1, 3}, {2, 4}]
Thread[f[f[1, 2], f[3, 4]] , f] ===> f[f[1, 3], f[2, 4]]
Thread is equivalent to Transpose if l is a matrix.
See also:
MapThread Transpose
-
Functions dedicated to the optics calculations and simulations in FFS.
-
AccelerateParticles does TrackParticles with acceleration in a ring for a given numbe
r of turns.
The adiabatic damping is automatically taken cared.
Usage: AccelerateParticles[beam_,mom_,{n_Symbol,nturn_},opt___]
where beam is a list of beam coordinates in the same format for TrackParticles. mom is an
expression
to determine MOMENTUM in each turn as a function of turn number n. nturn is the total numb
er of turns.
An option Synchronize specifies a routine to be executed at every turn of the tracking (e.
g. changing
voltages and magnet settings, or storing the results.)
Example:
AccelerateParticles[
beam,
Which[
n < 100, 1e9,
n <= 200, 1e9 + (n - 100) * 1e7,
True, 2e9],
{n, 300},
Synchronize :> ((
d = {d, MOMENTUM/1e9 * (1 + #2[[2,6,1]])})&)];
See also:
TrackParticles
-
BeamMatrix[i] returns a 6 by 6 beam-matrix (i.e., ) at location i. The index
i can have
a fraction to specify intermediate numbers (see LINE or Twiss). The calculation is based o
n linear
4 by 5 calculation in the present version, so the z-direction is meaningless. Flag GAUSS a
ffects
the result.
See also:
LINE Twiss GAUSS
-
Usage: DynamicApertureSurvey[range,nturn,options]
where
range: a list of {xrange,yrange,zrange}, with
xrange: {xmin, xmax},
yrange: {ymin, ymax},
zrange: {zmin, zmax},
and for the horizontal plane, specified by the Axes option,
the corresponding range must be given as {v1, ..., vn}.
These values are the initial amplitude divided by the equilibrium
values, i.e., Sqrt[2Jx,y/(EMITX+EMITY)], Sqrt[2Jz/EMITZ].
See EMITTANCE(EMIT) command or Emittance function.
nturn: number of turns to track.
options: Output->lfn : output to the unit lfn (see OpenWrite).
Axes->axes : one of "XY", "XZ", "YX", "YZ", "ZX", "ZY",
where the first character specifies the horizontal axis, and
the second the vertical, respectively. The default is "ZX".
ReferenceOrbit->{x0, px0, y0, py0, z0, dp0} : Survey is done around
this orbit.
PhaseX->phix : The initial amplitude is rotated in (X, PX) phase space
by phix. Default is zero.
PhaseY->phiy : The initial amplitude is rotated in (Y, PY) phase space
by phiy. Default is zero.
PhaseZ->phiz : The initial amplitude is rotated in (Z, PZ) phase space
by phiz. Default is -Pi/2.
ExpandElementValues->True(default) : set the values of the components
according to the values of elements. Machine errors may be reset.
See machine-error-commands, CALCULATE(CALC).
DynamicApertureSurvey returns the result as a list:
{score,{{{xmin, xmax},{ymin, ymax},{z1, z2, .., zn}},
{{z1,score1,{turn1_1,..,turn1_50}},..,
{zn,scoren,{turnn_1,..,turnn_50}}}}} ,
where score = Sum[scorei,{i,n}], scorei is the "score" of i-th momentum, and turni_j is th
e lost
turn of the particle with i-th momentum and j-th initial amplitude.
DynamicApertureSurvey tracks number of particles with different initial conditions in t
he range
given by range. It outputs a z-x diagram of the dynamic aperture of the ring. Fifty one in
itial conditions
are chosen in the range x-range for each point of z-range. The initial y-amplitude is line
arly dependent
on the x-amplitude. It tracks from xmax to downward for each z-amplitude zn, until the par
ticles
turns nturn with successive DAPWIDTH x-amplitudes. The default DAPWIDTH is 7.
DynamicApertureSurvey does parallel processing up to NPARA processes.
See also:
NPARA DAPWIDTH
-
Element[key-string, {element-pattern-string | element-position}] returns values for k
ey-string of
elements which match element-pattern-string or located at element-position. It returns a l
ist if
more than one elements match. The key-string and element-pattern-string can be symbols, un
less values
are not assigned to them.
If the second argument is omitted, it means all elements.
The element-position can be known by Element["POSITION"].
Key-strings "VALUE" and element-keywords allows to be set (i.e., Element[a,b] = v) when
element-pattern-string
chooses only one element. If a value is set to Element, it is automatically distributed to
all components
those belong to the element. If the keyword is the default variable, the error given by ma
chine-error-command
DK is applied.
The arguments of Element can be lists. It automatically maps as
Element[{a,b,c..},y] means {Element[a,y],Element[b,y],Element[c,y]..}
Element[x,{a,b,c..}] means {Element[x,a],Element[x,b],Element[x,c]..},
where both x and y can be also a list.
If an option Saved->True is given, Element refers the save-buffer which can be transfer
red to
other beam lines. Otherwise values set by Element are not saved when FFS is stopped, unles
s they
are the default-keyword or keywords once used in matching.
See also:
elements wildcards components LINE SetElement
-
The key-string is not case-sensitive. Available key-strings are:
"LENGTH" Number of elements in the beam line. No second argument.
"POSITION" Position of the element in the element-list.
"NAME" Name of the element.
"VALUE" Current value of the default keyword of the element.
"KEYWORDS" List of available keywords of the element.
"DEFAULT" The default keyword of the element
"TYPE" The internal code-number of the type of the element.
"TYPENAME" The name of the type of the element.
keyword If keyword is the default keyword, it means the current value. If not, it mean
s the saved
value. Changing the non-default keyword by Element does not affects the curren
t setting
of the components.
"EXPAND" Distribute the value of the default-keywords and the keywords used in the matc
hing to
all components in the beam line. No second argument.
Setting by Element["VALUE",..] or Element[keyword,..] to the DEFAULT keyword or a matchin
g-variable
keyword changes the current value, and distributed to the components in the succeeding ca
lculation.
See also:
set-value-of-element elements keywords default-keyword components
-
Emittance[option] returns a set of rules as
{keyword1->value1, keyword2->value2, ..} .
Its options and default values are Matrix(False), Orbit(False), OneTurnInformation(False),
Emittance(True),
ExpandElementValues(True), SaveEMIT(False), InitialOrbit(Null), InitialBeamMatrix(Null), a
nd Output(0).
If
Emittance->False is specified, the resulting keywords are:
Stable True if all modes are stable and the closed orbit is found.
Tunes {nux, nuy, nuz} .
EnergyLossU0 One turn energy loss in eV.
RfVoltageVc The effective RF voltage (V).
EquilibriumPosition dz in meter.
MomentumCompaction -dz/dp
OrbitDilation ds in meter.
BucketHeight dV/E0
HarmonicNumber The effective harmonic number
OrbitAtExit physical c.o.d. at the end of line.
If None of the options is given, the following keywords are added:
DampingRate {T0/taux, T0/tauy, T0/tauz}
Emittances {emitx, emity, emitz}
MomentumSpread sigma p/p0
BunchLength sigma_z
Polarization equilibrium polarization, if POL is on
Polarization2 equilibrium polarization by up to 2nd order calculation
Polarization4 equilibrium polarization by up to 4th order calculation
Polarization6 equilibrium polarization by up to 6th order calculation
PolarizationVector direction of polarization AppendTo the entrance of the beam line
SpinTune spin tune on the closed orbit
NominalSpinTune spin tune calculated by MOMENTUM and electron g-2
TuneShiftByRadiation {dnux, dnuy, dnuz}
If OneTurnInformation->True, or Orbit->True, or Matrix->True, the followings are added.
OrbitAtEntrance physical c.o.d. at the entrance of the ring.
OneTurnTransferMatrix symplectic part of the one-turn transfer matrix.
OneTurnDampingMatrix deviation of transfer matrix due to radiation.
NormalCoordinates conversion matrix from physical to normal coords.
OneTurnExcitation excitation matrix by radiation.
EquilibriumBeamMatrix equilibrium beam matrix.
ExtendedTwissParameters list of rules giving the extended Twiss parameters at the entranc
e of the
ring.
If Orbit->True or Matrix->True, the following is added:
ClosedOrbit List of physical closed orbit at every element in the ring.
If Matrix->True, the followings are added:
TransferMatrices List of physical transfer matrix from the beginning of the beam line
to all
elements.
IntrabeamExcitation List of the change of the 6 x 6 beam matrix due to the intrabeam scat
tering
(only when INTRA), converted to the beginning of the beam line.
If the flag TRPT or NORING is set, the calculation assumes a transport line so that sev
eral quantities
such as damping rate, eigen modes, equilibrium beam matrix, etc. are meaningless. Use RING
or NOTRPT
for such calculation. In the case of TRPT or NORING, the incoming beam envelope must be gi
ven by
the option InitialBeamMatrix with a 6 x 6 symmetric matrix. TRPT is useful for calculation
of space
charge and intrabeam in a transport line.
Please do not forget to put semicolon at the end of Emittance[] function, otherwise the
output
will be huge especially when Orbit or Matrix is True.
If ExpandElementValues->False, calculation is made using the present values of each compo
nent (i.e.,
including machine errors).
If SaveEMIT->True, the calculated values of emittances are stored in variables EMITX, EMIT
Y, EMITZ,
SIGE, SIGZ. The default is SaveEMIT->False.
InitialOrbit->{x0,px0,y0,py0,z0,dp0/p0} specifies the incoming orbit which is valid when N
OCOD is
set. The option Output->filenum enables the print out of EMITTANCE(EMIT) to filnum.
See also:
EMITTANCE(EMIT) SymplecticJ COD EMITX EMITY EMITZ SIGZ SIGE POL
-
With MAP elements, ExternalMap defines a user-defined map of particles. It also allow
s a user to
do anything (doing statistics, etc.) at any point of a beam line during a tracking.
Usage: First define a MAP element at MAIN level:
MAP name=(L=leng);
Right now L is the only keyword. Insert it at the location(s)
where you want to use it.
1) Tracking
In FFS, define the function ExternalMap as
ExternalMap["TRACK",n,nt_,x_]:=body;
The second argument n is the position of MAP counting from the beginning, which can be obt
ained using
LINE["POSITION","name.m"]. The third argument nt_ is used to receive the number of turns w
hich is
incremented by the tracking. The last argument x_ is used to receive the coordinates of pa
rticles.
It is a (7, np) list of real numbers. The elements (1..6, i) are (x, px ,y ,py ,z ,dp/p0)
of the
i-th particle. The (7, i) element is True(==1) if the i-th particle has been survived, an
d False(==0)
if it has been lost.
You can define ExternalMap to change the coordinates of each particle as you like by retu
rning a
new x in the same format as above. If you do not return it or you return in a different fo
rmat, the
tracking routine does not change the particle coordinates. You can neither rebirth a lost
particle
nor kill a surviving particle.
After defined ExternalMap, tracking calls it in every turn.
Example:
MAP P1=();
....
LINE A=(... P1 ... P1 ...);
....
FFS USE=A;
ExternalMap["TRACK",LINE["POSITION","P1.2"],nt_,x_]:=
(Print[x];x*2);
....
TRACK USE=A ....;
This example defines ExternalMap to print out the coordinates of all
particles at the second P1 in the line A. It also makes all coordinates
of all particles twice in every turn.
2) Emittance
In FFS, define the function ExternalMap as
ExternalMap["EMIT",n,cod_]:=body;
The second argument n is the position of MAP counting from the beginning, which can be obt
ained using
LINE["POSITION","name.m"]. The last argument cod_ is used to receive the orbit at the entr
ance of
the element, as a list of 6 real numbers. ExternalMap must return a list, either {cod1, tr
ans} or
{cod1, trans, dtrans, dbeam}, where cod1 is the orbit at the exit, trans is the 6 by 6 tr
ansfer
matrix of this element, dtrans is the radiation damping part of the transfer matrix (6 by
6), and
dbeam is the radiation excitation of the beam matrix (6 by 6). Only j >= i parts of dbeam[
[i, j]]
are taken into account.
Example:
ExternalMap["EMIT",LINE["POSITION","P1"],cod_]:=(
Print[cod];
{cod+{0,0.001,0,0,0,0},IdentityMatrix[6]});
3) Optics
In FFS, define the function ExternalMap as
ExternalMap["OPTICS",n,cod_]:=body;
The second argument n is the position of MAP counting from the beginning, which can be obt
ained using
LINE["POSITION","name.m"]. The last argument cod_ is used to receive the orbit at the entr
ance of
the element, as a list of 6 real numbers. ExternalMap must return a list {cod1, trans}, wh
ere cod1
is the orbit at the exit and trans is the 6 by 6 transfer matrix of this element. In the c
ase of
CACL4D (== ~CALC6D), only the 4 by 5 transfer matrix is effective.
Example:
ExternalMap["OPTICS",LINE["POSITION","P1"],cod_]:=(
Print[cod];
{cod+{0,0.001,0,0,0,0},IdentityMatrix[6]});
4) Geometry
In FFS, define the function ExternalMap as
ExternalMap["GEO",n,geo_,pos_]:=body;
The second argument n is the position of MAP counting from the beginning, which can be obt
ained using
LINE["POSITION","name.m"]. The argument geo_ receives the geometry of the beam line at the
MAP element,
in the same format as LINE["GEO",n], i.e., {{GX,GY,GZ},{CHI1,CHI2,CHI3}}. The last argumen
t pos_
receives the orbit length S at the element. ExternalMap must return an updated list {geo1,
pos1},
as { {{GX,GY,GZ},{CHI1,CHI2,CHI3}}, S} as the values at the exit of the element.
Example:
ExternalMap["GEO",LINE["POSITION","P1"],geo_,pos_]:=(
Print[cod];
{ {geo[[1]]+{1,0,0}, geo[[2]]}, pos+0.1})
See also:
MAP CALC4D
-
FFS[command-string] executes command-string as FFS commands. Any commands can be used
. Some commands
CALCULATE(CAL), GO, VARIABLES(VAR), SHOW returns their result, otherwise Null is returned.
All outputs
of the commands are suppressed.
FFS[command-string,lo] directs the output of the commands to file-number lo. The file-n
umber lo
may be given by OpenWrite or OpenAppend.
The IF structure and REPEAT(REP) loop must complete within a single FFS.
See also:
Input/Output OpenWrite OpenAppend
-
FFS["SHOW"] or FFS$SHOW[] returns the current matching conditions as a list. Each
element has
a form of
{component1, component2, function, goal-value, number-of-momentums, scale},
which corresponds to the format of the print-out by SHOW.
See also:
SHOW
-
Usage:
(1) FitValue[component, function, {id_,dp_}, goal_, now_] := body
modifies the goal of the matching of function at component. The argument id_ is the orbit
id for
MatchingAmplitude or InitialOrbits. The argument dp_ receives the value of dp/p0. The argu
ment goal_
is the value of the goal of the matching set by matching-function-commands. The argument n
ow_ is
the current value of function.
Example: FitValue["$$$", "NX", {_,dp_}, goal_, now_] := goal + dp * xix * 2 * Pi
sets the tune NX to have chromaticity xix.
(2) FitValue[component1, component2, function, {id_,dp_}, goal_, now1_, now2_] := body
modifies the value of the function at component1 for a two-component matching. Component1
is assumed
upstream in the beam line. The value of body is used in place of the current value, now1.
The argument
id_ is the orbit id for MatchingAmplitude or InitialOrbits. The argument dp_ receives the
value of
dp/p0. The argument goal_ is the value of the goal of the matching set by matching-functio
n-commands.
The argument now1 and now2 are the current values of the function at component1 and compon
ent2, respectively.
Example:
FitValue["QF1", "QF2", "NX", _, goal_, now1_, now2_] :=
If[Abs[now2-(now1+goal)] < 0.01*2*Pi , Null, now1]
sets the tune difference between QF1 and QF2 gaol +- 0.01.
During the matching process the matching routine calls FitValue with arguments, then if
body returns
a number, it overrides the goal give by matching-function-commands. If body returns Null,
the matching
of function is ignored.
The matching-function-command is necessary besides FitValue to perform the matching. On
ly defining
FitValue does not do the matching.
FitValue is cleared by USE. It is hidden by VISIT and restored by BYE
See also:
matching-function-commands off-momentum-matching
-
A defined function to modify the weight of matching of particular function at partic
ular component
with particular momentum offset.
Usage: FitWeight[component, function, {id_,dp_}, default_] := weight;
where
component is the name of the location of the fit, like "QF.2", etc.
function is the name of the matching-function, like "BX", "LENG", etc.
id_ is the id number of the orbit for MatchingAmplitude or InitialOrbits.
dp_ is a variable to receive the momentum deviation of the fit.
default_ is a variable to receive the default fit weight.
weight is an expression which returns the desired weight.
Example: FitWeight["$$$","LENG",{_,dp_},ws_]:=ws*10;
makes the weight of LENG at $$$ 10 times (100 times in MatchingResidual) bigger than the d
efault.
See also:
matching-function-commands special-variables MatchingResidual
-
GeoBase[{chi1, chi2, chi3}] converts the rotation angles of the coordinate base vecto
rs to a transformation
matrix {{x_gx,x_gy,x_gz}, {y_gx,y_gy,y_gz}, {z_gx,z_gy,z_gz}}
See also:
GEO OrbitGeo
-
LINE[key-string, {component-pattern-string | component-position}]
returns values for key-string of components which match component-pattern-string or locate
d at component-position.
It returns a list if more than one components match. The key-string and component-pattern-
string
can be symbols, unless values are not assigned to them. The second arg can be a fractional
number
to denote an intermediate value of two components.
If the second argument is omitted, it means all components.
The component-position can be known by LINE["POSITION"].
Key-strings "DIR" and component-keywords allows to be set (i.e.,
LINE[a,b] = v) when component-pattern-string chooses only one component.
The arguments of LINE can be lists. It automatically maps as
LINE[{a,b,c..},y] means {LINE[a,y],LINE[b,y],LINE[c,y]..}
LINE[x,{a,b,c..}] means {LINE[x,a],LINE[x,b],LINE[x,c]..},
where both x and y can be also a list.
See also:
components wildcards elements Element
-
The key-string is not case-sensitive. Available key-strings are:
"LENGTH" Number of components in the beam line. No second argument.
"POSITION" Position of the component in the beam line.
"NAME" Name of the component.
"TYPE" The internal code-number of the type of the component.
"TYPENAME" The name of the type of the component.
"ELEMENT" The name of the corresponding element.
"DIR" The orientation of the component, +-1.
"S" The orbit length to the entrance from the beginning of the beam line.
"LENG" Same as "S".
"GEO" Geometric-functions at the entrance of the component, {{GX, GY, GZ}, {GCHI1,
GCHI2,
GCHI3}}.
"OGEO" Geometric-functions of the orbit at the entrance of the component, {{OGX, OGY
, OGZ},
{OCHI1, OCHI2, OCHI3}}.
"GAMMA" Lorentz factor gamma.
"GAMMABETA" Lorentz factor gamma*beta = Sqrt[gamma^2 - 1].
"SIGab" Beam matrix component, where a and b are one of X, PX, Y, PY, Z, DP. If b is
omitted
it returns Sqrt[SIGaa] is returned. Just "SIG" returns the entire 6 by 6 beam
matrix.
"SIZEab" Beam matrix component calculated by (CODPLOT;EMIT), where a and b are one of
X, PX,
Y, PY, Z, DP. If b is omitted it returns Sqrt[SIZEaa] is returned.- "SIZE" re
turns the
entire 6 by 6 beam matrix.
"MULT" The ordered number of each component belonging to the- same element, starting
from 1.
keyword The value of the keyword of the component (see below).
"EXPAND" Distribute the value of the default-keywords and the keywords used in the mat
ching to
all components in the beam line. No second argument.
"GX", "GY", "GZ" Geometric functions GX, GY, GZ.
"GCHI1", "GCHI2", "GCHI3" Geometric functions CHI1, CHI2, CHI3
"OGX", "OGY", "OGZ", "OCHI1", "OCHI2", "OCHI3" Geometrical functions at the orbit.
Setting by LINE[keyword,..] to the DEFAULT keyword for the FIRST component changes the cu
rrent value
of the corresponding element, because the value of an element is stored in the first compo
nent.
See also:
components geometric-functions elements keywords default-keyword Element
-
Usage: OptimizeOptics[options]
optimizes (1 + MatchingResidual) or any function using DownhillSimplex with variables spec
ified by
FREE. Unlike GO, any keyword of any element can be a variable.
OptimizeOptics returns the final simplex. The variables are set to the values which giv
e the minimum
of the function so far at the end.
Options:
All options for DownhillSimplex are valid.
OptimizeFunction -> fun is the function to be minimized. The default is
((FFS["CALC"];1+MatchingResidual)&).
InitialSimplex -> initial sets the initial simplex to initial. The
default is Null, which mean to create initial from the current value
of the variables. Its format is same as for initial of
DownhillSimplex
SimplexSize -> size is the initial size of the simplex. Each variable
is relatively shifted by this amount from the current value.
Example:
free Q* Q* L
fit nx .3 ny .2
OptimizeOptics[]
optimizes the optics by changing the lengths of quads which are not allowed by GO, as well
as K1
of quads.
See also:
DownhillSimplex
-
OrbitGeo[location] returns the geometry {GX, GY, GZ} of the current (not design) orbit.
See also:
GEO GeoBase
-
To calculate the field of the synchrotron radiation from particles, first record traj
ectories of
particles. This is done by the function TrackParticles with a new flag RADLIGHT on. When R
ADLIGHT
is on, TrackParticles returns a list
{beam, trajectory} ,
where beam is a list as {location, coordinates}, and trajectory is a list
{ {t1 .. tm}, {x1 ..xm}, {y1 .. ym}, {z1 .. zm} }, ..
where {t,x,y,z}_i is the coordinates of the particle at i-th point in the trajectory. The
origin
and the direction of the spatial coordinates are the same as GEO coordinate {GX, GY, GZ}.
One can
track many particles at the same time by TrackParticles, so the trajectory has the dimensi
ons {np,
m}, where np is the number of particles.
After the trajectory is obtained, one can calculate the field in time domain
at any observation point. This is done by the function RadiationFiled as
field = RadiationField[ trajectory[[i]], obs];
where trajectory[[i]] is the trajectory of the i-th particle, and obs is the spatial coord
inate of
the observation point in the GEO coordinate. The output field is a list
{ {tau1 .. taum},
{Ex1 .. Exm}, {Ey1 .. Eym}, {Ez1 .. Ezm},
{Hx1 .. Hxm}, {Hy1 .. Hym}, {Hz1 .. Hzm},
{Sx1 .. Sxm}, {Sy1 .. Sym}, {Sz1 .. Hzm} }
where H = (n x E)/(c mu0) and S = E x H , and tau is the observation time.
RadiationField uses the Feynmann-Heviside formula
E = (mu0 e*CHARGE/4pi) (c^2n/R^2 + R/c d(c^2n/R^2)/dt + d^2n/dt^2) ,
where n and R are the direction vector and the distance from the electron at the retarded
time to
an observation point.
The derivatives in the above formula is calculated using the spline
interpolation.
Next one can calculate the spectrum of the field by RadiationSpectrum as
spect = RadiationSpectrum[ {field[[1]], field[[k]]},
{lambda1, lambda2, dlambda} ] ,
where filed[[k]] is one of the fields calculated by RadiationField. The range of the wavel
ength is
given as a list above. The output spectrum spect is a list as
{ {k1 .. kk}, {c1 .. ck}, {s1 .. sk} } ,
where k1 .. kk is the wave number k = omega/c, c1 .. ck and s1 .. sk are the cosine and si
ne integrals
of the field in tau1 .. taum , i.e.,
ck + I sk = Integrate[ field[tau] Exp[I c k tau] dtau] .
An example is seen in $(SAD_ROOTPATH)/sad/examples.sad .
See also:
TrackParticles RADLIGHT
-
To calculate the field of the synchrotron radiation from particles, first record traj
ectories of
particles. This is done by the function TrackParticles with a new flag RADLIGHT on. When R
ADLIGHT
is on, TrackParticles returns a list
{beam, trajectory} ,
where beam is a list as {location, coordinates}, and trajectory is a list
{ {t1 .. tm}, {x1 ..xm}, {y1 .. ym}, {z1 .. zm} }, ..
where {t,x,y,z}_i is the coordinates of the particle at i-th point in the trajectory. The
origin
and the direction of the spatial coordinates are the same as GEO coordinate {GX, GY, GZ}.
One can
track many particles at the same time by TrackParticles, so the trajectory has the dimensi
ons {np,
m}, where np is the number of particles.
After the trajectory is obtained, one can calculate the field in time domain
at any observation point. This is done by the function RadiationFiled as
field = RadiationField[ trajectory[[i]], obs];
where trajectory[[i]] is the trajectory of the i-th particle, and obs is the spatial coord
inate of
the observation point in the GEO coordinate. The output field is a list
{ {tau1 .. taum},
{Ex1 .. Exm}, {Ey1 .. Eym}, {Ez1 .. Ezm},
{Hx1 .. Hxm}, {Hy1 .. Hym}, {Hz1 .. Hzm},
{Sx1 .. Sxm}, {Sy1 .. Sym}, {Sz1 .. Hzm} }
where H = (n x E)/(c mu0) and S = E x H , and tau is the observation time.
RadiationField uses the Feynmann-Heviside formula
E = (mu0 e*CHARGE/4pi) (c^2n/R^2 + R/c d(c^2n/R^2)/dt + d^2n/dt^2) ,
where n and R are the direction vector and the distance from the electron at the retarded
time to
an observation point.
The derivatives in the above formula is calculated using the spline
interpolation.
Next one can calculate the spectrum of the field by RadiationSpectrum as
spect = RadiationSpectrum[ {field[[1]], field[[k]]},
{lambda1, lambda2, dlambda} ] ,
where filed[[k]] is one of the fields calculated by RadiationField. The range of the wavel
ength is
given as a list above. The output spectrum spect is a list as
{ {k1 .. kk}, {c1 .. ck}, {s1 .. sk} } ,
where k1 .. kk is the wave number k = omega/c, c1 .. ck and s1 .. sk are the cosine and si
ne integrals
of the field in tau1 .. taum , i.e.,
ck + I sk = Integrate[ field[tau] Exp[I c k tau] dtau] .
An example is seen in $(SAD_ROOTPATH)/sad/examples.sad .
See also:
TrackParticles RADLIGHT
-
Create/set/read a MAIN-level element.
Usage: SetElement[ element-name, element-type, options]
where
element-name: name of the element, either a symbol or a string
element-type: type of the element, a symbol, a string, or a number
options: one or more rules or list of rules of the form
keyword -> value or keyword :> value, to set the corresponding
value of keyword of the element.
SetElement returns a list of information of the element, in the suitable form for apply
ing SetElement
again.
You can define a new element by SetElement.
You can change the values of keywords of the element.
You cannot, however, change the type of an existing element, nor cannot delete the elem
ent.
The element-type can be Null. If so, a null type is assumed for a new element.
Examples:
LINE A = ( .. );
QUAD QF = (K1 = 0.2);
...
FFS USE = A;
...
SetElement["QF"] ! reads values of QF.
SetElement["QF","QUAD"] ! same as above.
SetElement["QF","BEND"] ! error because QF is QUAD.
SetElement["QF",,{"K1"->0.1}] ! set K1 of QF to 0.1 .
SetElement["QF","QUAD",{"K1"->0.1}] ! same as above.
!Assuming QF1 and QF2 are undefined yet:
SetElement["QF1","QUAD",{"K1"->0.1}] ! create a new QUAD QF1 with K1=0.1 .
SetElement["QF2",,{"K1"->0.1}] ! error because no type with key.
SetElement["QF2"] ! This is OK.
SetElement["QF2","QUAD"] ! Now the type of QF2 is defined.
See also:
elements keywords Element
-
SurvivedParticles[x]
returns the list of 6 coordinates and the flag of the survived particles in x. The form of
x is {x,
px/p0, y, py/p0, z, dp/p0, flag}, where each is a list of length of the number of particle
s. If all
particles are lost, it is a list of seven null lists.
See also:
TrackParticles
-
SymplecticJ[n] returns a n by n symplectic matrix like
{{0, 1, ...}, {-1, 0, ...}, {0, 0, 0, 1, ...}, {0, 0, -1, 0, ...}, ...} .
-
SynchroBetaEmittance calculates equilibrium emittance under influence of synchrotron
motion and chromaticity.
Usage:
SynchroBetaEmittance[{nus0, nus1, dnus},options]
or
SynchroBetaEmittance[nus0,options]
where nus0, nus1, and dnus are the starting, ending and step size of synchrotron tune, res
pectively.
If only nus0 is given, calculation is done only for nus0. The returned value is a list:
{{nus, emitx, emity, emitxp, emityp, conv}, ... }
where nus, emitx, emity, emitxp, emityp, conv are the synchrotron tune, equilibrium horizo
ntal and
vertical emittances, horizontal and vertical projected emittances, and the convergence, re
spectively.
When conv is negative, calculation failed to converge, and the returned emittances are not
reliable.
Options
Type Default Meaning
-----------------------------------------------------------
AzimuthalModes Real 9 Number of azimuthal modes
See also:
SYNCHTOBETA(SYNCHROB)
-
TouschekLifetime interpolates the data calculated by EMIT or Emittance[]. There are t
hree ways of
usage:
TouschekLifetime[Infinity, Infinity, nz]: Touschek lifetime in seconds
with momentum aperture nz * SIGE.
TouschekLifetime[nx, Infinity, nz]: Touschek lifetime in seconds
with acceptance 2Jx/(nx * (EMITX+EMITY)) + 2Jz/(nz * EMITZ) < 1.
TouschekLifetime[Infinity, ny, nz]: Touschek lifetime in seconds
with acceptance 2Jy/(ny * (EMITX+EMITY)) + 2Jz/(nz * EMITZ) < 1.
EMIT or Emittance[] with INTRA must precede TouschekLifetime.
See also:
EMITTANCE(EMIT) Emittance INTRA
-
TrackParticles[beam, destination-component, nbegin, nend]
returns a beam after the tracking at the entrance of the destination- component. The desti
nation
can be specified by the name of the component or by a number obtained by LINE["POSITION",
component].
If destination is omitted, the end of the line is assumed.
The argument nbegin is the initial turn number to be passed to tracking to indicate it is
in the
n-th turn. The number is increased by 1 when it passes the end of beam line. If nbegin is
omitted,
1 is assumed.
The argument nend is the last turn number. The default is nbegin.
The variable beam and also the result of TrackParticles are lists of the form
{location, coordinates}
where location is the position-number of the starting point. If location is same as or in
the downstream
of destination, the tracking is done by folding across the beginning of the beam line. The
coordinates
are in a list of {7, np} form, where np is the number of particles. The first 6 elements o
f coordinates
specifies
{x, px/p0, y, py/p0, z, dp/p0}
in this order. The {7, i} is the flag which is True(==1) when the particle is alive, and F
alse(==0)
when lost.
If the flag POL is on, TrackParticles performs spin tracking. Then the coordinates has
two more
components sy and phis, which correspond to the y-component of the classical spin vector a
nd the
angle ArcTan[sx, sz], respectively. If POL is on, another flag RADPOL turns on the Sokolov
-Ternov
effect.
When a flag RADLIGHT is on, TrackParticles returns the trajectories of particles which
are used
to calculate the radiation fields. See RadiationField and RadiationSpectrum.
When PHOTONS is ON (default is OFF), TrackParticles generates a list of all photons radiat
ed through
the tracking. The list is assigned to a symbol PhotonList.
See also:
components LINE PHOTONS PhotonList RADLIGHT TouschekLifetime WakeFunction SurvivedParticles
POL RADPOL
-
Twiss[optical-function, component] returns the value of the optical-function at the
entrance of
component. The values are those calculated by the last CALCULATE(CALC) or GO commands, or
CalculateOptics
function.
The second argument, component can be a name of component, a component number, or a list
of them.
If the number has a fraction, the intermediate value in the component is calculated.
Twiss["ALL",component] or Twiss["*",component] returns all 28 optical-functions at the en
trance
of component as a list:
{AX, BX, NX, AY, BY, NY, EX, EPX, EY, EPY, R1, R2, R3, R4, DETR, DX, DPX, DY, DPY, DZ, DDP
, AZ, BZ,
NZ, ZX, ZPX, ZY, ZPY},
which can be directly used in CalculateOptics. In the current version, however, parameters
after
AZ are uninteresting, because it always returns 1 for BZ and zeros for the others.
Keywords "PEX", "PEPX", "PEY", "PEPY", "PZX", "PZPX", "PZY", "PZPY" return dispersions
in the
physical coordinate.
Keywords "LENGTH", "GAMMA", "GAMMABETA", "S", "SIGab" return the same results as for th
e function
LINE.
The units of NX, NY, NZ are in radian.
See also:
optical-functions extended-Twiss-parameters CalculateOptics LINE
-
Usage: VariableRange[element, keyword ,v_] := expression
where the current value of the element:keyword is passed in v_, and expression should give
False
when the value is out of range.
Example: VariableRange["QF","ROTATE",v_]:= -0.1 < v < 0.1;
This restricts the range of the rotation angle of QF within +-100 mrad.
VariableRange[_,"ROTATE",v_]:= -0.1 < v < 0.1;
This specifies the same for all elements.
The expression can also return the range as a list {vmin, vmax}, which may give more ch
ance of
solution-finding for the matching routine.
VariableRange only acts for variables used in the matching with the FREE command.
See also:
FREE set-value-of-element
-
Usage: VariableWeight[element, keyword ,v_] := expression
where the default weight for matching with element:keyword is passed in v_, and expression
should
return a modified value of weight. If non-real is returned, the default weight is used.
Example: VariableWeight["QF","K1",v_]:= 0.1*v;
reduces the weight of QF1:K1 to 1/10 of the default value.
The weight also affects the step size of the numerical derivative of the response. A sm
aller weight
makes the step size larger.
VariableWeight only acts for variables used in the matching with the FREE command.
See also:
FREE set-value-of-element
-
WakeFunction[Longitudinal, comp]={{z1, wl1}, ..., {zn, wln}};
WakeFunction[Transverse, comp]={{z1, wt1}, ..., {zn, wtn}};
specify longitudinal and transverse dipole wake functions at a component comp (string). Ea
ch functions
is a list of {z, w} where z is the distance (z>=0) and w is the value of the wake, in the
unit of
either V/C or V/C/m.
The wake functions are applied at the component comp, giving kicks to each orbit whose
initial
conditions are given by InitialOrbits. The sufficient number of orbits depends on the situ
ation.
WakeFunction is valid only when TRPT and INS, and also either TWAKE or LWAKE is ON.
For tracking, it is only valid in TrackParticles.
See also:
TrackParticles TRPT INS TWAKE LWAKE
-
Graphics represents an object for 2D graphics with the form
Graphics[primitives, options]. Up to now available primitives are:
Circle[{cx,cy},rx, options] : Circle.
Circle[{cx,cy},{rx,ry}, options] : Oval.
Points[{{x1,y1} .. {x2,y2}}, options] : Points.
Points[{{x1,y1,dx,dy} .. {x2,y2,dx,dy}}, options] : Points with error bars.
Line[{{x1,y1} .. {x2,y2}}, options] : Line.
Line[{{x1,y1,dx,dy} .. {x2,y2,dx,dy}}, options] : Line with error bars.
Rectangle[{x1,y1}, {x2,y2}] : A box.
Rectangle[{x1,y1}, {x2,y2}, graphic] : Graphics in a box.
Polygon[{{x1,y1} .. {x2,y2}}, options] : Polygon.
Text[{string, {x,y}}, options] : Text-string at {x,y}.
Possible options and their defaults values of Graphics are:
option default optional values
------------------------------------------------
AspectRatio GoldenRatio any positive number
DisplayFunction $DisplayFunction Identity or Null to suppress display
Detach False True to run tdr asynchronously
Epilog {} List of primitives
Frame True False to erase outline, ticks, ticklabels.
FrameClick True to allow click on frame to change options.
FrameLabel {"","","",""} List of strings
FrameTicks {Both,Both,Ticks,Ticks}
None to turn off ticks and labels
Both to turn on ticks and labels
Ticks to turn on ticks only
<< For bottom tick >>
False is same as Ticks
True is same as Both
<< For top tick >>
False is same as None
True is same as Ticks
<< For left & right ticks >>
False is same as None
True is same as Both
If a form {___, _List} is given where
the List is a list of {coord, label, opt___}
label is displayed at coord with option opt.
If a form {___, fun} is given and
fun[coord,exp,org] returns a list of options
for Canvas[Create$Text], it is displayed at major
ticks at coord. exp is the exponent and org is the
original label.
GridLines Automatic Automatic to draw grid lines at major ticks
{Automatic,None} for only x
{None,Automatic} for only y
Both, Minor, and Major can be also used.
PlotLabel "" string
PlotRange Automatic {ymin,ymax} or {{xmin,xmax},{ymin,ymax}}
Prolog {} List of promitives
Scale {Linear,Linear} Log, Date
TickSize 1 relative size of ticks.
FrameThickness Automatic thickness of the frame line incl. ticks.
Legend "" shows legend-string.
FontScale 1 Relative size of fonts for FrameLabel, FrameTicks.
FrameFontScale 1 Relative size of fonts for FrameLabel.
If Real, applied to all frames. If List, applied to
bottom, left, top, right, supplemented 1s to the right.
TickFontScale 1 Relative size of fonts for FrameTicks.
If Real, applied to all frames. If List, applied to
bottom, left, top, right, supplemented 1s to the right.
LegendFontScale 1 Relative size of fonts for Legend.
Options for primitives:
For Text:
option default optional values
------------------------------------------------
TextAlign "" "CENTER"
TextCases "" string to represent CASES of TopDrawer
TextPosition "" "DATA" to represent the position by data
coordinates
TextRotate 0
TextSize 1 relative size of a character
PlotColor "Black" one of "White", "Black", "Red",
"Green","Blue","Yellow",
"Magenta","Cyan"
For Point
option default optional values
------------------------------------------------
PointSize 1 relative size of a point
PointSymbol "1O" Symbol for PLOT of TopDrawer, or Bar
"6O","7O","8O","9O" are triangles
in CanvasDrawer.
PlotColor "Black" one of "White", "Black", "Red",
"Green","Blue","Yellow",
"Magenta","Cyan"
ErrorBarTickSize 1 length of error bar ticks.
For Line
option default optional values
------------------------------------------------
Dashing "1" character string or a list of numbers to
represent the dashing of the line.
Plot True whether plot symbols at data points.
If True, PointSize and PointSymbol are
effective (see above).
PlotColor "Black" one of "White", "Black", "Red",
"Green","Blue","Yellow",
"Magenta","Cyan"
ErrorBarTickSize 1 length of error bar ticks.
Thickness 1 thickness of line
For Polygon
option default optional values
------------------------------------------------
Plot False whether plot symbols at data points.
If True, PointSize and PointSymbol are
effective (see above).
PointSize 1 relative size of a point
PointSymbol "1O" Symbol for PLOT of TopDrawer, or Bar
"6O","7O","8O","9O" are triangles
in CanvasDrawer.
PointColor "forest green" point fill color.
PointBorderColor Automatic point border color.
Automatic measn PointColor.
PointTags Null points tag string or list of tag strings.
PlotJoined True whether plot border line of polygon.
Thickness 1 thickness of border line
Dashing "1" character string or a list of numbers to
represent the dashing of the line.
PlotColor "black" border line color.
LineTags Null border line tag string.
FillColor Null polygon fill color.
Null means empty polygon.
Tags False polygon tag string.
ListPlot accepts options for Graphics, Point, and Line. Show accepts
options for Graphics. The output is written to file #9 (fort.9 in OSF1 and
ftn09 in HP-UX) in TopDrawer commands. If SAD is running on X, the plot is
also done immediately.
Examples:
g1=ListPlot[{{1,2},{10,20}},Scale->Log,PlotJoined->True,
DisplayFunction->Identity];
g2=ListPlot[{{1,15},{10,3}},Scale->Log,PlotJoined->True,Dashing->"1 0.3",
DisplayFunction->Identity,Plot->False];
g3=ListPlot[{{1,2.5},{5,10},{10,12}},Scale->Log,
DisplayFunction->Identity];
Show[g1,g2,g3,FrameLabel->{"X (mm)","Log(Y)"},PlotLabel->"Test Plot",
AspectRatio->1];
-
Usage: BeamPlot[loc, axes, options]
plots a beam ellipse at a location loc, for axes. Axes are given by a list
{ax, ay}, where ax and ay are one of "X", "PX", "Y", "PY", "Z", "DP".
The beam envelope should be calculated by (CODPLOT;EMIT) or BEAM commands before
BeamPlot.
options defaults
-----------------------------------------
Orbit True Uses Twiss["DX",loc], etc. as the center of
ellipse.
SizeFunction "SIZE" If "SIG", LINE["SIG"] is used.
LINE["SIZE"] is the default.
AspectRatio 1
DataRange Default If Default, PlotRange becomes square for
axes = {"X", "Y"} or {"PX", "PY"}
See also:
BEAMSIZE(BEAM) EMITTANCE(EMIT) CODPLOT
-
Usage: ColumnPlot[data, options, ...]
plots a column plot.
1) If data is a 1D vector, it makes a simple column plot.
2) If data is a 2D matrix, it makes a multiple-column plot.
3) If data is a 3D list, it makes a stacked, multiple-column plot.
Besides options common for all plotting functions, ColumnPlot has its own
options:
Option Value Default Action
---------------------------------------------------------------------------
ColumnOffset 0 < number < 1 0.15 Ratio of spacing of columns
Reference number 0 Where column starts
Orientation Vertical Vertical Orientation of columns
Horizontal
ColumnLabel List of Str. Automatic Labels for each column
Function Scale for column number
None No labels
FillColor color Colors to fill columns
list of colors
MeshStyle bitmap Bitmap to fill columns
list of bitmaps to distinguish stacking
TextSize positive number 1 relative label size
Example:
g=ColumnPlot[{{{1,1,2},{2,2,3}}, {{1,4,2},{2,2,3}}, {{1,3,2},{2,2,3}}}, Orientation->Hor
izontal];
Update[];
See also:
Graphics
-
Usage: FitPlot[data, fun, var, {par1,ini1}, .. , {parn, inin}, opt].
See also:
Fit
-
Usage: GeometryPlot[options]
plots a geometry of beam line.
options defaults
-----------------------------------------
Region {1,LINE["LENGTH"]} {begin, end}, begin and end can be strings.
Both begin and end point of drawing region
could be given by "S" unit by using S[begin|end] form.
Names "*" A pattern of component names to be plotted.
See also:
Graphics OpticsPlot
-
Usage: HistoPlot[data, options, ...]
plots a histogram using ColumnPlot(default) or ListPlot.
Data can be a single list, or list of lists, which results in a multi-column histogram on
a common
axis.
Besides options common for all plotting functions and ColumnPlot, it has its own options:
Option Value Default Action
---------------------------------------------------------------------------
Bins number Automatic number of bins
BinRange {min,max} Automatic Range of bins
PlotStyle ColumnPlot ColumnPlot plot function
ListPlot
FitPlot
Orientation Vertical Vertical orientation of columns
Horizontal
FitParameters args for FitPlot in a list
See also:
Graphics ColumnPlot ListPlot FitPlot
-
Usage: ListContourPlot[list, options, ...]
plots a contour plot by list which is a 2D List of Real data.
Option Value Default Action
---------------------------------------------------------------------------
Contours Real 10 number of contours
PlotRange {min,max}, {prxy, prz}, or {prx, pry, prz}
Automatic depth of contours (prz) and PlotRange fo
r x-y (prxy)
AspectRatio
Real 1
MeshRange ({x1,xn},{y1,yn}} or {{x1,..,xn},{y1,..,y1n}}
Automatic Range of x and y axes
ColorFunction Color scheme (Blue, Purple, Pink, Yellow, Green, Cyan),Function, or Strin
g
Blue Null or None means "white"
ContourColorFunction
Function or String
Automatic Null or None to hide
ColorScale True or False True displays a color scale on the right
Smoothing integer >= 0 1 number of linear interpolations
Example:
xr0=0;xr=Table[xr0+=Sin[i*Pi/21],{i,20}];xr-=(xr[[1]]+xr[[-1]])/2;
yr=xr;
table=Outer[Cos[Sqrt[(#^2+#2^2)/2]]&,xr,yr];
gc=Graphics[MapThread[
Rectangle[#2,#3,
ListContourPlot[table, MeshRange->{xr, yr}, AspectRatio->1,
DisplayFunction->Identity, ColorFunction->#,
FrameLabel->{"x", "y", ToString[#]}]]&,
{{ Blue, Pink, Green, Purple, Yellow, Cyan},
{{-0.15,0.65},{0.25,0.65},{0.65,0.65},{-0.15,0 },{0.25,0 },{0.65,0}},
{{ 0.2, 1.1 },{0.6, 1.1 },{1, 1.1 },{ 0.2, 0.45},{0.6 ,0.45},{1.0, 0.45}}}]];
Show[gc];Update[];
See also:
Graphics ListPlot ListDensityPlot
-
Usage: ListDensityPlot[list, options, ...]
plots a density plot by list which is a 2D List of Real data.
Option Value Default Action
---------------------------------------------------------------------------
PlotRange {min,max}, {prxy, prz}, or {prx, pry, prz}
Automatic depth of contours (prz) and PlotRange fo
r x-y (prxy)
AspectRatio
Real 1
MeshRange ({x1,xn},{y1,yn}} or {{x1,..,xn},{y1,..,y1n}}
Automatic Range of x and y axes
ColorFunction Color scheme (Blue, Purple, Pink, Yellow, Green, Cyan),Function, or Strin
g
Blue Null or None means "white"
Mesh True or False False True to draw mesh
MeshColor Function or String
Automatic Null or None to hide
ColorScale True or False True displays a color scale on the right
Smoothing integer >= 0 1 number of linear interpolations
Example:
data = Table[Sin[x]/Cos[x^2 + y^2], {x, -2, 2, 0.1}, {y, -2, 2, 0.1}];
ListDensityPlot[data,PlotRange->{-5,5}, MeshRange->{{-2,2},{-2,2}}, FrameLabel->{"x","y
"}];
Update[];
See also:
Graphics ListPlot ListContourPlot
-
Usage: ListPlot[{{x1,y1},..,{xn,yn}}, options]
makes a graphic with points.
ListPlot[{y1,..,yn}, options] assumes 1,..n for the x-xoordinate.
ListPlot[{{x,y,dy}, ..}, options ] plots error bars of length dy in y.
ListPlot[{{x,y,dx,dy}, ..}, options ] plots error bars in x and y.
option default optional values
------------------------------------------------
PlotJoined False True
Step
StepRatio 1 ratio of stepping position
between two data points
Type ? to see other options for Graphics.
Example:
data1={{1,2},{3,5},{4,-1}};
data2={{1,4},{2,-2},{3.5,3},{5,3}};
g1=ListPlot[data1, PointColor->"dark slate blue",PlotJoined->True, Thickness->2, PlotCol
or->"dark
slate blue", FrameLabel->{"x","y"}, Legend->"data1", DisplayFunction->Identity];
g2=ListPlot[data2, PointColor->"tomato", Legend->"data2", DisplayFunction->Identity];
Show[g1,g2];
Update[];
See also:
Graphics Plot
-
Usage: OpticsPlot[fun_list, options]
makes a plot of built-in optical functions, user-defined functions, or
list of data at components on the beam line. The parameters are:
fun_list: a list of objects to be plotted in a window. The number of windows in a plot i
s the length
of fun_list object plotted in a window MUST have same dimensions. An element o
f fun_list
is one of fun_label, fun, list_data or a list as {object, options}, where
fun_label: one of "AX", "BX", "NX", "EX", "EPX", "DX", "DPX", "AY", "BY", "NY", "EY", "EP
Y", "DY",
"DPY", "R1", "R2", "R3", "R4", "DETR", "AZ", "BZ", "NZ", "ZX", "ZPX", "ZY", "Z
PY", "DZ","DDP","PEX",
"PEPX", "PEY", "PEPY", "GAMMA", "GAMMABETA","SIGab", where a and b in "SIGab"
are one
of X, PX, Y, PY, Z, DP.
fun: Any function of the component number. A fractional number may be used to obt
ain the
intermediate value.
list_data: a list of {{pos1, val1}..{posn,valn}}.
options defaults
-----------------------------------------
Region {1,LINE["LENGTH"]} {begin, end}, begin and end can be strings.
Both begin and end point of drawing region
could be given by "S" unit by using S[begin|end] form.
Lattice True False to turn of drawing lattice
LatticeRegion Automatic {low,high}, the region where lattice is drawn
FrameHeight Automatic List of relative heights of each frame
InfoLabel False If True, pressing Button shows Twiss, etc.
Names "*" A pattern of component names to be plotted.
RemoveOverlap "L$NAME" If not "L$NAME", overlapping of lattice names
remain untouched.
Tags False True to attach tags "C$"//(component name)
to each rectangle for the lattice, and
"L$"//(component name) to the component
label (CanvasDrawer only).
Legend False If Automatic, Legend is composed from FrameLabel
Automatically.
options in a fun_list element:
options defaults
-----------------------------------------
Unit 1 Unit of the object. "Meter", "InvMeter",etc.
FrameLabel "" Left frame label.
Legend False If Automatic, Legend is composed from FrameLabel
Automatically.
Example:
p2=OpticsPlot[{{"BX","BY"}, {"DX",{{{10,0.001},{20,0.002}}, FrameLabel->"DX meas.", Uni
t->Meter,
Thickness->2, Names->"Q*"}}}];
Update[];
See also:
Graphics ListPlot
-
Usage: Plot[fun, range, options] or Plot[{fun1, .. }, range, options],
where fun is a function and range is a list given as {x, xmin, xmax}.
options defaults
-----------------------------------------
MaxBend 0.04
PlotPoints 25
PlotDivision 250
Dashing {"1","0.8 0.24","0.4 0.12","0.2 0.08","0.1 0.08",
"0.8 0.08 0.08 0.08","0.4 0.08 0.08 0.08"}
Options for ListPlot and Graphics are also available
The independent variable should have been cleared (i.e., no value should
not be set) when Plot is called.
Example:
ff[x_]:=Sin[x]/x;
ff[0]=1;
Plot[{Cos[x],ff[x]}, {x,0,10}, Thickness->2];
Update[];
See also:
Graphics ListPlot
-
-
$FORM is a character-string to specify the format of the output of a real number.
Usage: $FORM="w.f"
$FORM="Sw.f"
$FORM="Fw.f"
$FORM="Mw.f"
where w is the width of the output, and f is the length of the fractions. If S is attached
, trailing
zeroes are omitted. If F is attached, it becomes same as FORTRAN's F-format. If M is attac
hed, the
exponent is expressed as 10^n. If w and f are omitted, 17.15 is assumed.
The default is S17.15 .
-
$Input holds the file number for console input stream. The default is -1.
See also:
$Output
-
$Output holds the file number for console output. The default is -1.
See also:
$Input
-
Close[f] closes file number [f]. It is necessary to complete the output to an extern
al file.
Close[f1, ...] and Close[{f1, ...}] close all files f1, ...
See also:
OpenRead OpenWrite OpenAppend OpenShared StringToStream
-
f = OpenAppend[file]
opens file (_String) for write and returns the file number (_Real)
See also:
Close OpenRead OpenWrite
-
f = OpenRead[file]
opens file (_String) for read and returns the file number (_Real)
See also:
Close OpenWrite OpenAppend
-
f = OpenWrite[file]
opens file (_String) for write and returns the file number (_Real)
See also:
Close OpenRead OpenAppend
-
PageWidth is the number of columns of the output. The default is set from GetEnv["WIDTH"].
-
Print[expr1 [,expr2 ...]]
converts expr1... to _String then write them to $Output. A newline character is appended a
t the end.
See also:
Write WriteString
-
Read[f, item [, item1...] [, opts..]]
reads item from file number f. item can be one of or a list of:
Word a word, delimited by WordSeparators
Real a real expression
Expression an expression
Character a single character
A format n*item is possible with a positive integer n.
A list {item1,.., itemn} is possible. The result is also a list.
opts are options given by a Rule:
Option Value Default Effect
WordSeparator _String " ,\t"
the delimiters for Word
ReadNewRecord True/False True If true, read the next record of the file beyond
the end
of line
See also:
OpenRead Close
-
ReadString[f]
reads the next record from file number f, and returns it as a _String.
See also:
Read OpenRead Close
-
StandardForm[expr]
resets $FORM and PageWidth to their defaults, then evaluate expr, returns the result, and
resets
$FORM and PageWidth to those at the beginning of StandardForm.
See also:
$FORM PageWidth
-
f = StringToStream[string]
opens a character string for read and returns the file number (_Real)
See also:
Close
-
Write[f, expr1 [,expr2 ...]]
converts expr1... to _String then write them to file number f. A newline character is appe
nded at
the end.
See also:
WriteString Print OpenWrite OpenAppend Close $FORM PageWidth StandardForm
-
WriteString[f, expr1 [,expr2 ...]]
converts expr1... to _String then write them to file number f. No newline character is app
ended.
See also:
Write OpenWrite OpenAppend Close $FORM PageWidth StandardForm
-
-
Forks the process into a parent and a child processes.
Fork[]
returns 0 and the child's pid for the child and the parent, respectively.
-
Allocated shared memory of n bytes.
s = OpenShared[n] ,
where s is a file number to be used by Shared function. The allocated memory can be releas
ed by Close[s].
-
Read/Write to the shared memory.
Shared[s]
Shared[s] = x
Shared[s] := x
where s is given by OpenShared, and x is Real, built-in function, String, defined symbol,
or list
of them.
-
Returns the size of an object for OpenShared.
n = SharedSize[x]
-
Environment for an object-oriented-programming is supplied by:
Class: The function to define a class.
context: A class defines a context to define its all symbols for
the variables and methods within the context.
This automatically avoids conflicts of symbols between
classes, Global, and System. When c = Class[ ... ] is
done, a context c` is defined.
members: The set of Members of a class is a union of class variables,
instance variables, and class methods of the class.
operator @: A special operator to access class member. In a notation
f@g, g's context defaults the class of the class of f.
f@g@h[x] is recognized as ((f@g)@h)[x] , thus the context of
h defaults the class of f.
superclasses: A class inherits all class variables, instance variables,
class methods from its superclasses which are give by the
first argument of Class. If a null list is given, Object`
is set as the default superclass. Multiple inheritance is
allowed.
class variable: Class variables are given by the second argument of Class
as a list of symbols. They are unique in the class.
They can be initialized by declaring in a way such as
{a=1, {b, c} = {2, 3}} like Module. A form like
{a = b = c =1} is allowed.
instance variable:
Instance variables are given by the third argument of Class
as a list of symbols. An instance has those symbols
separately. They can be initialized by declaring in a way
such as {a=1, {b, c} = {2, 3}} like as Module. A form like as
{a = b = c =1} is allowed. Also they
are initialized at the creation of instance by rules as
x = c[ a->1, b:>Print[d]], etc.
class methods: Class methods are given by the fourth(last) argument of
Class. They must be in the form of either one of
f_[arg___] := g_;
With[_, f_[arg___] := g_];
With[_, f_[arg___] := g_; .. ];
If[_,
ft_[argt___] := gt_; ..,
ft_[argf___] := gf_; ..,];
h_[f_[arg___], b___] ^:= g_; .
where f is the symbol for the method to be defined.
Set may be used instead of SetDelayed if necessary.
This: A symbol This in the definition of the method, it is
translated to the object (the instance or the class) which
refers the member.
default reference:
In the definition of the class methods, whenever a member of
the class is appeared, it is recognized as This@member.
When a symbol of the member conflicts the symbol in System`,
the system symbol should be wrapped by Literal.
reference of member of superclasses:
Members of the superclasses (denote cc) are referred by
cc`member in the definition of the method.
copying an instance:
An instance c of a class can be copied to another symbol
by c1 = c. After the copying, c1 and c refer the identical
instance. Destructing one of them by such as c1=. clears
the instance and also all the assigned symbols.
Constructor: When an instance is defined, by x = c[arg], a method
x@Constructor[arg] is always invoked.
In evaluation of instance definition under class scope,
class member symbol appeared 1st slot of Rule or RuleDelayed
argument is sent to Constructor of new class instance
without evaluation. (In other term, class member symbol on
1st slot of Rule or RuleDelayed argument behaves like
evaluating with implicit Literal[]) One can configure
Constructor[] in the definition of the class.
x = c[arg] returns the returned value of Constructor[arg].
The rules in the argument work in two ways: (1) A rule for an
instance variable or a class variable sets the initial value
of the variable, (2) Other rules are stored in an instance
variable Options as a list.
Destructor: An instance x is cleared by (x=.), which invokes
x@Destructor[]. The default Destructor is Object`Destructor,
but one can reconfigure it in the definition of the class.
Short: When an instance x is returned as the result of expression
for Out[], x@Short[] is invoked to show the result. The
default Short is Object`Short, but one can reconfigure it
in the definition of the class.
other methods: Class[] gives the class of the instance.
Parents[] gives the immediate superclasses.
AllParents[] gives the all superclasses.
Members[] gives a list of class variables, class methods,
and instance variables of the class.
AllMembers[] gives a list of class variables, class methods,
and instance variables of the class and its all parents.
See also:
Member(@)
-
Class sets up a class of objects.
Usage: a = Class[
list of superclasses,
list of class-variables,
list of instance-variables,
class-methods];
Example: a = Class[
{aa, bb}, (* aa and bb are superclasses *)
{a1, a2}, (* class-variables *)
{v1, v2}, (* instance-variables *)
Constructor[arg__] := (Print[{arg}]; v1 = Plus[arg]);
sum[] := v1 + v2 (* defining Constructor and method "sum"*)
];
a1 = a[1, 2] (* creating an instance of a *)
a1@v1 (* accessing an instance variable *)
a1@v2 = 3 (* setting an instance variable *)
a1@sum[] (* calling a method "sum" *)
a1=. (* delete an instance *)
-
The random number functions use common seed given by SEED command or SeedRandom funct
ion. It has
an initial value 17 at the beginning of FFS. The cut-off value of GaussRandom[] is given b
y variable
GCUT.
See also:
special-variables: GCUT
-
Random[] gives a uniform random number between 0 and 1.
Random[n] gives a list of n uniform random numbers.
Random[n1, n2, ..] gives a (n1 * n2 * .. ) tensor of uniform random numbers.
See also:
GaussRandom ParabolaRandom SeedRandom
-
GaussRandom[] gives a Gaussian random number with average 0,
standard deviation 1, cutoff at GCUT.
GaussRandom[n] gives a list of n Gaussian random numbers.
GaussRandom[n1, n2, ..] gives a (n1 * n2 * .. ) tensor of Gaussian random
numbers.
See also:
Random ParabolaRandom SeedRandom
-
ParabolaRandom[] gives a parabola random number between -1 and 1.
ParabolaRandom[n] gives a list of n parabola random numbers.
ParabolaRandom[n1, n2, ..] gives a (n1 * n2 * .. ) tensor of parabola random
numbers.
See also:
Random GaussRandom SeedRandom
-
SeedRandom[plugin_String] selects new pseudo random-number generator
plugin named as plugin.
SeedRandom[seed_Real] initializes the internal state of the current
pseudo random-number generator plugin by seed.
SeedRandom[{seeds__Real}] initializes the internal state of the current
pseudo random-number generator plugin by {seeds}.
SeedRadnom[state_List] restores both the selection of the pseudo random-number
generator plugin and the internal state of the selected
plugin by using state dumped by SeedRandom[].
SeedRandom[] returns List containing both the current selected pseudo
random-number generator plugin name and its internal state.
See also:
ListRandom Random GaussRandom ParabolaRandom
-
ListRandom[] returns List of available pseudo random-number generator plugins.
See also:
SeedRandom
-
-
-
DateString[] returns the current date and time as string "mm/dd/CCYY HH:MM:SS".
DateString[date] converts date to string as above. The date can be either a real number (
in second,
date=0 is 1/1/1900 0:0:0) or a list of 6 reals {Y,m,d,H,M,S}.
-
MemoryCheck[n]
checks the consistency of the memory allocation by SAD. The range of the check and the out
put depend
on n:
MemoryCheck[] : checks the consistency of the free area and returns the allocation info,
MemoryCheck[1] : checks the consistensy of the free and used areas. Returns the allocatio
n info.
MemoryCheck[2] : checks the consistensy of the free and used areas. Returns the allocatio
n info.
and a list of free segments.
The returned value is {used, allocated from system, # of free segments, missing size[, li
st of free
segments]} in units of word (= 8 bytes).
If an inconsistency is found, messages are printed out.
-
TimeUsed[] returns the cputime since the start of SAD in seconds.
See also:
Timing
-
Timing[fun]
evaluates fun and returns {cputime, result}. cputime is in seconds.
See also:
TimeUsed
-
TracePrint[fun]
prints out all function calls and each expression compound in ";" in the evaluation of fun
.
Usage: (1) FIT [component]
(2) FIT component1 component2
sets the current location where the matching condition is applied. The component is given
with the
form name[.order][{+-}offset] (see components). If component is omitted, the end of the be
am line
is chosen.
If two components are given, it means a relative-fitting or zone-fitting. If the fittin
g condition
is not maximum-fitting, the condition means to make values at two components equal (for AX
, BX, AY,
BY, EX, EPX, EY, EPY, R1, R2, R3, R4, DX, DPX, DY, DPY, PEX, PEPX, PEY, PEPY, CHI1, CHI2,
CHI3),
or have the specified difference (for NX, NY, LENG, GX, GY, GZ). If the fitting condition
is maximum-fitting,
the condition means a zone-fitting (for AX, BX, AY, BY, EX, EPX, EY, EPY, R1, R2, R3, R4,
DX, DPX,
DY, DPY, PEX, PEPX, PEY, PEPY, CHI1, CHI2, CHI3), which suppress the maximum of the functi
on in the
region between component1 and component2, or maximum-fitting for the difference of the fun
ction (for
NX, NY, LENG, GX, GY, GZ). The fit region is shown in the first part of the prompt when F
FSPRMPT
is ON.
Examples: (1) FIT QF.2-10
sets the current fit point at 10 components upstream from the entrance of the second QF.
(2) FIT QF QD NX 0.5 BXM 10
sets the two-point fitting between QF and QD, then set the difference of NX between QF and
QD to
be 0.5, and the maximum of BX to be 10 in the region between QF and QD.
See also:
matching-function-commands components SHOW GO CALCULATE(CAL)
Usage: FITP n
sets n to the number of off-momentum points in the off-momentum matching. If the fitting
condition
is on-momentum only, it is not affected.
See also:
matching-function-commands
Usage: (1) FIX element-pattern [keyword] [element-pattern1 [keyword1]..]
removes elements which match element-pattern from the matching variables. The optional key
word specifies
the non-default variables. If the keyword is omitted, all keywords are removed.
For the MARK element at the beginning of the beam line, a special form can be used for
the FIX
command. That is a form I (appending "I" to a matching-function name).
Example: FIX AXI BXI AYI BYI
removes incoming AX, BX, AY, and BY from the matching variables.
Usage: (2) FIX
sets the standard optics for the orbit correction commands.
See also:
FREE FIT SHOW GO CALCULATE(CAL) wildcards elements
Usage: FREE element-pattern [keyword] [element-pattern1 [keyword1]..]
specifies elements which match element-pattern as the matching variables. The optional key
word specifies
the non-default variables. See default-keyword.
For the MARK element at the beginning of the beam line, a special form can be used for
the FREE
command. That is a form I (appending "I" to a matching-function name)
which means
the incoming condition of the matching-function is varied in the matching.
Example: FREE AXI BXI AYI BYI
changes incoming AX, BX, AY, and BY to find the solution.
See also:
FIX FIT SHOW GO CALCULATE(CAL) wildcards elements
-
The default and available non-default variable keywords are:
type default-keyword non-default variable keyword
DRIFT L -
BEND ANGLE K1,K0,E1,E2
QUAD K1 ROTATE
SEXT K2 ROTATE
OCT K3 ROTATE
DECA K4 ROTATE
DODECA K5 ROTATE
MULT K1 K0,K2..K21,SK0,SK1,SK2..SK21,ROTATE,ANGLE
MARK - AX,BX,EX,EPX,AY,BY,EY,EPY,R1,R2,R3,R4,DETR,
DX,DPX,DY,DPY,DZ,DDP,AZ,BZ,ZX,ZPX,ZY,ZPY
See also:
keywords
Available geometric-functions are:
GX geometrical coordinate xi
GY geometrical coordinate eta
GZ geometrical coordinate zeta
CHI1 geometrical rotation angle ch1_1
CHI2 geometrical rotation angle ch1_2
CHI3 geometrical rotation angle ch1_3
The geometrical coordinate {xi, eta, zeta} is set by the ORG command, and its default orig
in is at
the entrance of the beam line, and the default directions are xi in s-direction, eta in -(
x-direction),
and zeta in -(y-direction) at the entrance. The set {xi, eta, zeta} forms a right-hand sys
tem.
The rotation angles are defined so as to give the local {x,y,s} is written
{x, y, s}_local
= rotate[s, chi3] rotate[x, chi2] rotate[y, -chi1]{x, y, s}_origin,
where rotate[a, b] reads "rotate around the new-a vector by b right-handedly".
See also:
optical-functions matching-function-commands DISPLAY(DISP) GEOCAL GEOFIX
prints out the TopDrawer commands for the geometric plot of the beam line.
See also:
DISPLAY(DISP)
Usage: GO [[NO]EXPAND]
Does matching for fitting conditions given by matching-function-commands with variables sp
ecified
by FREE.
If an option EXPAND is given (default), it expands the beam line before the calculation. I
f NOEXPAND
is given, it avoids any expansion. FFS["CAL"] and FFS["GO"] returns the result as a list
, whose
format is
{dp, kind, reslist, function-values},
where
dp: a list contains dp/p0 .
kind: a list of kind of the orbit (usually 0, but 1 to 6 for the finite amplitude matc
hing, see
MatchingAmplitude).
reslist: a list of {residual, xstab, ystab}, where
residual: matching residual,
xstab: True when the matrix is stable in X,
ystab: True when the matrix is stable in Y, for each orbit.
Above are lists with length nf (== number of orbits).
function-values: a list of length nc (== number of calculated items). Each element has the
form:
{component1, component2, function, list-of-values},
where
component1, component2: fit locations (see FIT).
function: name of the function (see matching-function-commands).
list-of-values: list of the value of the function for each orbit Length nf.
The central orbit comes at the Floor[(n+1)/2]-th element.
See also:
FIT SHOW matching-function-commands off-momentum-matching FREE FIX VARIABLES(VAR) COUPLE(COUP)
ATTRIBUTE(ATTR) CALCULATE(CAL) VARY SHOW CONV CONVERGENCE MatchingResidual MatchingAmplitude
FitFunction FFS OptimizeOptics
Usage: IF expr1 body1 [ELSEIF expr2 body2 [ELSEIF ..]] [ELSE body3] ENDIF
This is a FORTRAN77 like IF-structure. If the expression expr1 is True(==1) or nonzero, ex
ecutes
commands in body1. If it is False(==0), skip commands until ELSE, ELSEIF or ENDIF appears
at the
same level of the IF-structure, and executes commands after ELSE or ENDIF, or executes the
ELSEIF
command. If expr1 is not a real number, an error message is printed and ignores the comman
d line.
See also:
ELSE ELSEIF ENDIF expression command-syntax If
IN {filename | file-number} switches the input stream to the specified file or the fi
le-number. The
original stream is kept and to be returned by TERMINATE(TERM). The input file is not rewou
nd.
See also:
TERMINATE(TERM) CLOSE(CLO) READ OUTPUT(OUT) APPEND(APP) END
Usage: machine-error-command [options] amount component-pattern ..
where machine-error-command is one of
command keyword affected applicable types
DELX DX BEND QUAD SEXT OCT DECA DODECA SOL CAV
DELY DY BEND QUAD SEXT OCT DECA DODECA SOL CAV
DL L DRIFT SOL
DTHETA ROTATE QUAD SEXT OCT DECA DODECA CAV
DTHETA DROTATE BEND
DK default-keyword DRIFT BEND QUAD SEXT OCT DECA DODECA MULT SOL CAV
DDK K0 or DBZ BEND SOL
amount is the amount of the error,
component-pattern is the pattern to specify the components to be applied.
Options are
RANDOM(R) Set amount*GaussRandom[] to the keyword.
UNIFORM(U) Set the specified amount to the keyword without random number.
INCOHERENT(INC) GaussRandom[] is called for each component. Default.
COHERENT(C) GaussRandom[] is called once for each component-pattern.
PUT(P) Set the error to the keyword. Default.
ADD(A) Add the error to the keyword.
See also:
components wildcards keywords default-keyword DUMP SEED
Usage: (1) matching-function goal-value [off-momentum-points]
(2) matching-functionM goal-value [off-momentum-points]
(3) matching-functionI incoming-value
(4) matching-functionSCALE scale
(1) sets the matching condition for matching-function at the current fitting point or regi
on with
the goal-value and the off-momentum-points (see off-momentum-matching).
If off-momentum-points is omitted, the previous value for this matching-function at thi
s fitting-point
is assumed. If the previous value is not defined, 1 is assumed. If -1 is given for off-mom
entum-points,
the matching-function is rejected from the matching (see REJECT(REJ)).
If "*" is given for goal-value, the previous value is used if exists.
Example: BX 10 3 (beta_x to be 10 at 3 momenta)
BX 20 (now beta_x to be 20 at 3 momenta (previous setting))
BX * 5 (now beta_x to be 20 (previous setting) at 5 momenta)
(2) If the letter "M" is appended to matching-function, it means the maximum-fitting for t
he function.
The maximum of either the value (for positive-definite functions) or the absolute value (f
or bipolar
functions) are to be limited in the matching.
(3) If the letter "I" is appended to matching-function, it specifies the value of the inco
ming beam.
(4)
If SCALE is appended to matching-function, it sets the scale of the input/output of the fu
nction
to scale. This scale is used in the matching-function commands, DISPLAY(DISP), SHOW, etc.
(5) If the current fit location is at a MARK, @ for the goal value refers the save value a
t the MARK.
@- refers -(save value). These are useful to match between two beam lines.
Available matching-functions are:
optical-functions (see optical-functions):
AX BX NX AY BY NY EX EPX EY EPY R1 R2 R3 R4 DETR DX DPX DY DPY DZ DDP PEX PEPX PEY PEPY TR
X TRY LENG
geometric-functions
(see geometric-functions):
GX GY GZ CHI1 CHI2 CHI3
See also:
FIT GO SHOW MARK optical-functions geometric-functions off-momentum-matching x-y-coupling
REJECT(REJ) special-variables DP functions FitValue MatchingAmplitude
The multi-turn tracking can be done by the TRACK command of the MAIN level, the TRACK
command in
FFS, or the DynamicApertureSurvey[] function in FFS. The latter only perform the DAPERT mo
de.
The multi-turn tracking uses the closed orbit, normal coordinate, and the equilibrium e
mittances.
Therefore One of EMITTANCE(EMIT), the Emittance[] function, or the EMIT command in the MAI
N level
are necessary to be done once in prior to the multi-turn-tracking. The values of EMITX, EM
ITY, EMITZ,
SIGE can be changed between EMITs and the multi-turn-tracking.
See also:
EMITTANCE(EMIT) RFSW RAD FLUC RADCOD SPAC WSPAC special-variables
Usage: MATRIX [{SYMPLECTIC(S) | PHYSICAL(P)}] [from to]
prints out the 4 by 5 (w/CALC4D) or 6 by 6 (w/CALC6D) transfer matrix from from-component
to to-component.
If SYMPLECTIC(S) is specified (default), the symplectic transfer matrix on {x,px/p0,y,py/p
0,dp/p0}
where p0 is the nominal momentum at the entrance, is given. Otherwise, in the case of TRPT
, the transfer
matrix on {x,px/p0(s),y,py/p0(s),dp/p0(s)} is printed out.
If the from- and to- components are omitted, entire beam line is assumed.
If to-component is upstream the from-component, it gives the inverse matrix (TRPT) or one-
turn-wrapped
matrix (RING).
See also:
DISPLAY(DISP) TRPT RING CALC4D CALC6D TransferMatrix
Usage: MEA [end-component] [OUT file plot-spaces]
tracks particles from the entrance to end-component and prints out the statistics at the e
nd. If
end-component is omitted, the component end used in the last MEASURE(MEA) (default: end of
the beam
line) is assumed.
If OUT file plot-spaces are attached, it plots phase space distribution on file. The ph
ase-spaces
are specified like as X-PX,
or X-Y, etc., (up to any numbers).
Parameters for the tracking are specified by special-variables and flags:
seed for the random-number generator:
SeedRandom[seed_Real] or SeedRandom[{seeds__Real}]
special-variables (can be set with =):
NP number of particles
EMITX horizontal emittance
EMITY vertical emittance
DP relative momentum spread
DP0 relative momentum offset dp/p0
GCUT cut-off value of the Gaussian tail
flags:
GAUSS/UNIFORM Gaussian/uniform(default) momentum distribution
JITTER/NOJITTER off(default)/on nullifying the incoming centroid offset
RFSW/NORFSW switch on(default)/off the rf-cavities
RAD/NORAD synchrotron radiation on/off
RADCOD/NORADCOD off/on compensation of energy loss due to radiation
FIXSEED/MOVESEED keep(default)/unkeep the initial random-number seed
The initial transverse distribution is Gaussian.
See also:
special-variables TrackParticles SeedRandom RESULTOFTRACKING
FFS matches the optical functions for an orbit with finite momentum deviation.
Example:
DP=0.01; sets the range of momentum to DP0-0.01 < dp/p0 < DP0+0.01 .
BX 10 9; sets the goal of betax to 10 m, at 9 points.
in the range above, i.e.,
dp/p0 = {-0.01,-0.0075,-0.005,-0.0025,0,
0.0025,0.005,0.0075,0.01} + DP0 .
GO starts the matching.
As this example, the off-momentum points are chosen with equal separation. If the off-mome
ntum point
n is an even number, the chosen points are same as the case of n+1, but the on-momentum po
int (==DP0)
is excluded.
See also:
matching-function-commands DP DP0
Available optical functions for matching are:
AX alpha_X
BX beta_X
NX psi_X, the default scale is 1/(2Pi)
AY alpha_Y
BY beta_Y
NY psi_Y, the default scale is 1/(2Pi)
EX eta_X (dispersion_X)
EPX eta_Px (dispersion_PX)
EY eta_Y (dispersion_Y)
EPY eta_Py (dispersion_PY)
R1 R_1 (see x-y-coupling)
R2 R_2 (see x-y-coupling)
R3 R_3 (see x-y-coupling)
R4 R_4 (see x-y-coupling)
DETR R_1*R_4 - R_2*R_3 (see x-y-coupling)
DX dx
DPX dpx
DY dy
DPY dpy
DZ dz
DDP delta=dp/p0
AZ alpha_Z
BZ beta_Z
NZ psi_Z, the default scale is 1/(2Pi)
ZX zeta_X (z-dispersion_X)
ZPX zeta_Px (z-dispersion_PX)
ZY zeta_Y (z-dispersion_Y)
ZPY zeta_Py (z-dispersion_PY)
PEX eta_x (dispersion_x)
PEPX eta_px (dispersion_px)
PEY eta_y (dispersion_y)
PEPY eta_yy (dispersion_py)
TRX trace(T_X), only defined at the end of the beam line.
TRY trace(T_Y), only defined at the end of the beam line.
LENG length of the design orbit
In the above, upper case X, Px, Y, Py represents the x-y decoupled coordinate. EX, EPX, EY
, EPY refer
the decoupled coordinate, while PEX, PEPX, PEY, PEPY are in the physical coordinate. On th
e other
hand, DX, DPX, DY, DPY refer the physical coordinate.
See also:
geometric-functions x-y-coupling matching-function-commands GO CALCULATE(CAL) DISPLAY(DISP)
SHOW
Usage: ORG location, dgx, dgy, dgz, dchi1, dchi2, dch3
sets the origin of the geometrical coordinate relative to the location with a relative shi
ft (dgx,
dgy, dgz) and rotation (dchi1, dchi2, dchi3).
OUT {filename | file-number} switches the output stream to the specified file or the
file-number.
The file is written from the beginning.
See also:
TERMINATE(TERM) CLOSE(CLO) INPUT(IN) READ APPEND(APP) END
Pattern is a special expression for mathing arguments in function definitions and ru
les with several
forms:
_ matches any single argument.
__ matches a sequence of 1 or more arguments.
___ matches a sequence of 0 or more arguments.
x_ matches any single argument, which is names x.
x__ matches a sequence of 1 or more arguments, which is named x.
x___ matches a sequence of 0 or more arguments, which is named x.
x:pattern a pattern which is named x.
pattern:v a pattern which has a default value v when matching is failed.
pattern.. a non-null sequence of arguments each of which matches pattern.
pattern... a sequence, which can be null, of arguments each of which matches pattern.
expression matches expression.
See also:
MatchQ defining-functions rules
Physical constants available in FFS are:
SpeedOfLight 299792458
FineStructureConstant alpha
ElectronCharge e in Coulomb
ElectronMass m_e in eV
ElectronRadius classical radius of electron, in m
ElectronGminus2 electron g-2
ProtonMass m_p in eV
ProtonRadius classical radius of Proton, in m
SIMu0 4 Pi 10^{-7}
SIEpsilon0 1/SIMu0/SpeedOfLight^2
BoltzmannConstant k_B in J/K
See also:
constants expression special-variables
PRI expression evaluates expression and prints out the result.
See also:
expression Print
Exits FFS and return to SAD/MAIN level, without saving the values of the elements.
See also:
STOP SAVE ABORT USE VISIT BYE
RADINT prints out the radiation integrals involving the x-coupling for all components
of the beam
line.
READ {filename | file-number} switches the input stream to the specified file or the
file-number.
The original stream is kept and to be returned by TERMINATE(TERM). The input file is rewou
nd.
See also:
TERMINATE(TERM) CLOSE(CLO) INPUT(IN) OUTPUT(OUT) APPEND(APP) END
REC exchanges the values of FREEd elements with those when the last GO command was is
sued. FIXed
elements are not affected.
See also:
GO FREE FIX RESET SAVE
Usage: (1) REJ matching-function-pattern [matching-function-pattern1..]
(2) REJ TOTAL
(3) REJ TOTALFIT
rejects the matching-functions which match matching-function-pattern at the current FIT lo
cation.
If TOTAL or TOTALFIT is given, the entire matching conditions in all locations are rejecte
d, then
output parameters by CALCULATE are reset when TOTAL is given.
See also:
matching-function-commands FIT wildcards
Usage: REP [n] body UNTIL [expr1]
executes commands in body n times until expr1 gives nonzero. The number n can be any expre
ssion which
gives a number. If n is omitted, infinity is assumed. If expr1 is omitted, False(==0) is a
ssumed.
See also:
UNTIL
Usage: RESET [ALL] [element-pattern]
restores the value of the elements. What are restored are the value of the default keyword
of all
elements, the values of the non-default keywords which have been changed manually or by th
e matching.
If ALL is given, it resets all keywords. If element-pattern is given, reset is limited to
the elements
which match the pattern.
See also:
SAVE USE VISIT wildcards RECOVER(REC)
REV changes the sign of AX, AY, EPX, EPY, R2, R3, DPX, DPY at the
entrance of the beam line.
See also:
matching-function-commands
Usage: element-pattern [keyword] [{MIN | MAX | MINMAX | MAXMIN}] value
sets value to the specified keyword of the elements which match element-pattern. If keywor
d is omitted,
the default-keyword is assumed. keyword can be a wildcard to apply all matching keywords.
If MIN, MAX, MINMAX, MAXMIN are specified, it sets the limit of the default-keyword. Bo
th MINMAX
and MAXMIN means MIN=-Abs[value] and MAX=+Abs[value].
If the keyword is not the default-keyword, it affects both the current and the saved va
lue.
See also:
ATTRIBUTES(ATTR) SAVE elements default-keyword wildcards Element
-
Available keywords are:
type keywords
DRIFT L RADIUS
BEND L ROTATE DROTATE DX DY ANGLE K0 K1 E1 E2 AE1 AE2 F1 FB1 FB2 FRINGE DISFRIN DISRAD
EPS RANKICK
QUAD L ROTATE DX DY K1 F1 F2 FRINGE DISFRIN DISRAD EPS
SEXT L ROTATE DX DY K2 DISFRIN DISRAD
OCT L ROTATE DX DY K3 DISFRIN DISRAD
DECA L ROTATE DX DY K4 DISFRIN DISRAD
DODECA L ROTATE DX DY K5 DISFRIN DISRAD
MULT L DX DY DZ CHI1 CHI2 ROTATE(=CHI3) K0..K21 SK0..SK21 DISFRIN F1 F2 FRINGE DISRAD E
PS VOLT
DVOLT HARM PHI DPHI FREQ RADIUS ANGLE E1 E2 AE1 AE2 DROTATE
SOL BZ DX DY DZ DPX DPY BOUND GEO CHI1 CHI2 CHI3 DBZ DISFRIN
CAVI L ROTATE DX DY VOLT DVOLT V1 V20 V11 V02 FREQ PHI HARM RANVOLT RANPHASE DISFRIN FR
INGE
TCAVI L ROTATE DX DY K0 V1 FREQ PHI HARM RANKICK RANPHASE
COORD DX DY CHI1 CHI2 CHI3 DIR
MARK AX BX AY BY EX EPX EY EPY R1 R2 R3 R4 DETR DX DPX DY DPY DZ DDP AZ BZ NZ ZX ZPX ZY
ZPY EMITX
EMITY DP AZ SIGZ GEO OFFSET
APERT DX1 DX2 DY1 DY2 DP AX AY DX DY
See also:
default-keyword set-value-of-element Element
-
The default and available non-default variable keywords are:
type default-keyword non-default variable keyword
DRIFT L -
BEND ANGLE K1,K0,E1,E2
QUAD K1 ROTATE
SEXT K2 ROTATE
OCT K3 ROTATE
DECA K4 ROTATE
DODECA K5 ROTATE
MULT K1 K0,K2..K21,SK0,SK1,SK2..SK21,ROTATE,ANGLE
MARK - AX,BX,EX,EPX,AY,BY,EY,EPY,R1,R2,R3,R4,DETR,
DX,DPX,DY,DPY,DZ,DDP,AZ,BZ,ZX,ZPX,ZY,ZPY
See also:
keywords
There are several variables which have special rolls in FFS. Some of them are also ac
cessible in
the MAIN level.
See also:
constants expression flags
-
%Line counts the number of the results in FFS Shown with Out[]:= . Out remembers all
outputs up
to Out[$Line]. $Line = 0 resets the counter and forgets the outputs.
-
CASE is a character-string to be attached with TITLE to issue the CASE command of Top
Drawer in DRAW
or GEO commands.
See also:
TITLE DRAW GEO
-
CHARGE contains the charge of the particle. The default is +1.
-
CONVERGENCE is the goal of the convergence(==MatchingResidual) in the matching. If Ma
tchingResidual
becomes smaller than CONVERGENCE times the effective number of the conditions, the matchin
g by GO
terminates. The flag CONV is set when MatchingResidual is smaller than CONVERGENCE after G
O or CALCULATE(CAL).
The default value is 10^-9.
See also:
GO MatchingResidual CONV
-
DAPWIDTH is the successive width of the x-amplitudes to terminate the tracking assumi
ng that the
aperture is enough. The default is 7.
See also:
DynamicApertureSurvey
-
DP represents the relative momentum spread of the beam. It is automatically set by th
e keyword DP
of the MARK element at the beginning of the beam line. The value of EMITY affects the defa
ult weight
of variables in the matching. In the off-momentum matching, the range DP0 - DP < dp/p0 < D
P0 + DP
is used for the matching. The assumed momentum-distribution in the BEAMSIZE(BEAM), MEASURE
(MEA),
etc. commands, is Gaussian with the standard deviation DP and the mean DP0 if the flag GAU
SS is on,
otherwise uniform (square) in the range DP0 - DP < dp/p0 < DP0 + DP.
See also:
DP0 off-momentum-matching GAUSS UNIFORM elements MARK
-
DP0 represents the central value of the relative momentum offset in the optics calcu
lation, or the
center of the momentum distribution of the beam. The on-momentum optics has the relative m
omentum
deviation dp/p0 == DP0, and the off-momentum calculation is done in the range DP0 - DP < d
p/p0 <
DP0 + DP.
DP0 sets the momentum deviation of the closed orbit at the entrance for EMIT with RADTAPE
R.
See also:
DP off-momentum-matching matching-function-commands EMITTANCE(EMIT) RADTAPER
-
DTSYNCH is the equilibrium arrival time advance (= -c*delta t, in meter) where the s
ynchrotron radiation
loss balances with the RF, calculated by EMIT/Emittance[SaveEMIT->True]. This corresponds
to the
origin of the RF phase. The default is zero.
See also:
EMITX EMITY EMITZ SIGZ SIGE EMITTANCE(EMIT) Emittance PHICAV
-
The effective angular frequency weff (= 2 Pi EFFRFFREQ) is obtained using the second
derivative
d^2Vcacc/dt^2 == -weff^2 Vcacc ,
ehere Vcacc is the total acceleration voltage at the equilibrium phase PHICAV. These quant
ities Vcacc
and its derivatives are summed over all CAVIs and MULTs.
It is set by EMITTANCE(EMIT) or Emittance[]. Effective with RING only.
See also:
EFFVC PHICAV
-
Effective peak rf voltage EFFVC is given by
Abs[ weff Vcacc + I dVcacc/dt ] / weff ,
where Vcacc, weff are total acceleration voltage at the equilibrium phase PHICAV and the e
ffective
RF angular frequency (=2 Pi EFFRFFREQ). DVcacc/dt is the time derivative of Vcacc. The qua
ntity Vcacc
and its derivatives are summed over all CAVIs and MULTs.
It is set by EMITTANCE(EMIT) or Emittance[]. The unit is Volt. Effective with RING only.
See also:
EFFVCRATIO EFFRFFREQ PHICAV
-
Ratio of (effective voltage)/(Sum[VOLT_k,{k}]) (default: 1). Set by EMITTANCE(EMIT)
or Emittance[].
Effective with RING only.
See also:
PHICAV EFFVC
-
ElementValues is a symbol to assign rules to determine values of keywords of elements
or components.
This is used to give a dependence between keywords of different elements or components, or
determine
then by a parametric expression.
Useage: ElementValues = { key[elem] :> expr, ...}
where
key: keyword to specify a value (string).
elem: String to specify the elements or components, wildcards are allowed.
expr: an expression which returs a real number to be set to the elements or components.
Example: ElementValues =
{ "DX"["QF1"] :> "DX"["QD1"]-0.001,
"DY"["QF2.3"] :> -"DY"["QD1.2"],
"ROTATE"["QF*"] :> f[x] }
Remarks:
1. Iff elem contains ".", it is recognized as components, otherwise as elements.
2. In the r.h.s. of the rule, an expression like key[elem] is evaluated as either LINE[ke
y, elem]
or Element[key, elem], depending on elem has ".".
3. The expression expr can be any expression returning a real number.
4. Later rules overrides the former, if many rules apply on the same keyword of the same
element.
5. The rule given by ElementValues overrides the relation given by COUP_LE command.
6. Use a[b] in stead of a@b.
7. ElementValues is cleared by USE. It is hidden by VISIT and restored by BYE.
See also:
COUPLE(COUP)
-
EMITX is a real variable for the horizontal emittance (not normalized by gamma beta).
It is automatically
set by the keyword EMITX of the MARK element at the beginning of the beam line. The EMITTA
NCE(EMIT)
command returns its calculated value in EMITX. The value of EMITX affects the default weig
ht of variables
in the matching. Accessible in MAIN.
See also:
EMITY EMITZ SIGZ SIGE DP elements MARK
-
EMITXE specifies the minimum horizontal emittance for EMITTANCE(EMIT) and Emittance[]
calculations.
It is useful to give emittance determined externally, such as for proton machines.
See also:
EMITYE EMITZE
-
EMITY is a real variable for the vertical emittance (not normalized by gamma beta). I
t is automatically
set by the keyword EMITY of the MARK element at the beginning of the beam line. The EMITTA
NCE(EMIT)
command returns its calculated value in EMITY. The value of EMITY affects the default wei÷
ht of variables
in the matching. Accessible in MAIN.
See also:
EMITX EMITZ SIGZ SIGE DP elements MARK
-
EMITYE specifies the minimum vertical emittance for EMITTANCE(EMIT) and Emittance[] c
alculations.
It is useful to give emittance determined externally, such as for proton machines.
See also:
EMITXE EMITZE
-
EMITZ is a real variable for the longitudinal emittance (not normalized by gamma beta
). It is automatically
set by the keyword EMITZ of the MARK element at the beginning of the beam line. The EMITTA
NCE(EMIT)
command returns its calculated value in EMITZ. Accessible in MAIN.
See also:
EMITX EMITY SIGZ SIGE DP elements MARK
-
EMITZE specifies the minimum longitudinal emittance for EMITTANCE(EMIT) and Emittance
[] calculations.
It is useful to give emittance determined externally, such as for proton machines.
See also:
EMITXE EMITYE
-
The exponent to calculate MatchinResidual. The default is 2.
See also:
MatchingResidual GO
-
If False (default), the calculation of response matrix for each matching variables us
es analytical
expressions as much as possible. If True, performs numerical differentiation during the ma
tching
by GO. It is useful for some variables and matching functions in some cases. It is slow, s
o should
be avoided for off-momentum-matching for a large beam line.
See also:
GO off-momentum-matching
-
FitFunction is a symbol to assign user-defined functions for matching with the GO com
mand.
Usage: FitFunction := fun,
where fun is a function that returns a real number or a list of real numbers, to be matche
d to zero
by GO. The goal of GO is to make fun zero or a list of zeros, together with built-in match
ing conditions.
Thus the sum of fun^2 is added to MatchingResidual. GO also evaluates FitFunction to obtai
n the derivatives
numerically. The function fun can refer the value of variables by Element or LINE function
s, and
the optical functions at DP0 by Twiss. The algorithm of matching is same as that for built
-in conditions,
but it is slower because of the numerical differentiation, when the beam line is long and
the number
of variables large.
Example: FitFunction := {Twiss["BX","$$$"]-20, Twiss["BY","$$$"]-20};
which puts the same goal as
FIT $$$ BX 20 BY 20 .
FitFunction is cleared by USE. It is also hidden by VISIT and restored by BYE.
See also:
GO FREE MatchingResidual DP0 Element LINE Twiss
-
FSHIFT is the relative shift df/f0 of the revolution (or rf) frequency in a ring. Thi
s is valid in
EMITTANCE(EMIT), the particle-tracking, and CAL/GO with CALC6D. For CAL/GO with CALC4D, DP
0 should
be used instead.
See also:
EMITTANCE(EMIT) CALCULATE(CAL) GO CALC6D CALC4D DP0
-
GCUT specifies the cut-off value of Gaussian distribution in unit of the standard dev
iation. Accessible
in MAIN.
See also:
SEED GAUSS GaussRandom
-
Usage: InitialOrbits = { {x1, px1, y1, py1, z1, dp1}, ...};
or InitialOrbits = { {ax1, bx1, nx1, ay1, by1, ny1,
ex1, epx1, ey1, epy1, r11, r21, r31, r41,
x1, px1, y1, py1, z1, dp1, 0, 0, 0, 0, 0, 0, 0}, ...};
specifies initial conditions of a number of orbits for the optics calculation by CALCULATE
(CAL) and
GO. Those coordinates are offset from the central orbit. If six numbers are given, only th
e offsets
of the orbits are affected. If 27 numbers are given, all Twiss parameters are set (values
for non-orbit
params are used directly. Orbits are giving offsets.)
If InitialOrbits are given, the off-momentum matching and finite-amplitude matching is d
isabled.
InitialOrbits is also necessary to calculate optics with wake field.
See also:
CALCULATE(CAL) GO off-momentum-matching finite-amplitude-matching
-
LOSSAMPL is the transverse amplitude beyond which a particle is judged to have been l
ost. The default
is 1 m. Accessible in MAIN.
See also:
LOSSDZ APERT
-
LOSSDZ is the longitudinal position z beyond which a particle is judged to have been
lost. The default
is 100 m. Accessible in MAIN. LOSSDZ is effective only when SPAC is ON.
See also:
LOSSAMPL APERT SPAC
-
MatchingAmplitude is a list of amplitudes for the finite-amplitude matching.
Usage: MatchingAmplitude := { {dp1,x1,y1}, ..};
where dp1 is the momentum deviation to be matched, x1 and y1 are the horizontal and vertic
al amplitudes
at the beginning of the beam line, normalized by Sqrt of the sum of the emittance, i.e., S
qrt[(EMITX+EMITY)].
Three orbits are chosen in each dimension. The initial conditions of the orbit is chosen a
s
{X,Px,Y,Py} =
{ {x1,0,0,0}, {-x1/2,Sqrt[3]/2 x1,0,0}, {-x1/2,-Sqrt[3]/2 x1,0,0},
{0,0,y1,0}, {0,0,-y1/2,Sqrt[3]/2 y1}, {0,0,-y1/2,Sqrt[3]/2 y1} },
and when x1==0 or y1==0 corresponding orbits are excluded. The above are labeled {x1,x2,x3
,y1,y2,y3}
in the output of CALCULATE(CAL) or GO, and also labeled 1 to 6 in the second element of FF
S["CALC"]
and FFS["GO"].
This matching is done when dp1 is within the off-momentum range given by DP, i.e., Abs
[dp1] <
DP. If dp1 is in the range, the nearest zero- amplitude optics is chosen. The maching cond
itions
for the finite- amplitude optics are same as those for the zero-amplitude one.
Th orbit with finte initial condition never close after one revolution, but FFS simply
ignores
it and obtain the periodic optics around the open
orbit.
See also:
DP EMITX EMITY off-momentum-matching CALCULATE(CAL) GO
-
MatchingResidual holds the convergence in the last GO or CALCULATE(CAL) commands. It
is calculated
by
sw*(Sum[(w_i*df_i)^ExponentOfResidual,{i}]/sw)^(2/ExponentOfResidual)
+penalty
where w_i is the weight of the i-th condition, df_i is the difference of the i-th functio
n from
the goal, penalty is an additional big number (typically 10), when the optics is unstable
or closed
orbit is not found in the case of CELL. The parameter sw is defined as
sw=Sum[(OffMomentumWeight/2/woff)^2,{i}]
with
woff = 1 for on-momentum optics
= Sqrt[number-of-momentum-points] for off-momentum optics.
The weight of the function is lighter in the case of off-momentum-matching so that all of
f-momentum
deviations functions weight equal to the on-momentum one. However, the relative weight for
the off-momentum
part can be changed by setting OffMomentumWeight.
The weight of each function at each point with each momentum can be specified by defini
ng the
FitWeight function.
See also:
ExponentOfResidual CONVERGENCE OffMomentumWeight off-momentum-matching FitWeight
-
MASS is the rest mass of the particle in eV. The default is the electron mass.
-
MINCOUP is the minimum emittance ratio (EMITY/EMITX) to be assumed in the calculation
of intrabeam
effects in EMITTANCE(EMIT). Accessible in MAIN.
See also:
EMITTANCE(EMIT) INTRA
-
MOMENTUM is the nominal momentum of the beam line at the entrance in eV/c. Accessible
in MAIN.
-
NBUNCH is the number of bunches for the calculation of WakeFunction. Accessible in MAIN.
See also:
PBUNCH
-
The net residual of convergence except the penalty for unstable optics.
See also:
MatchingResidual StablilityLevel
-
NP is the number of particles in the tracking. Accessible in MAIN.
See also:
MEASURE(MEA)
-
NPARA specifies the maximum number of parallel processes for various calculations suc
h as CALC, GO,
TrackParticles, DynamicApertureSurve, etc.
See also:
CALCULATE(CAL) GO TrackParticles DynamicApertureSurvey
-
Relative weight of the off-momentum deviation for the off-momentum matching. The defa
ult is 1.
See also:
ExponentOfResidual CONVERGENCE MatchingResidual off-momentum-matching FitWeight
-
OMEGA0 is 2*Pi*SpeedOfLight/LINE["s","$$$"] . Accessible in MAIN.
See also:
SpeedOfLight LINE
-
OpticsEpilog is a variable to assign a user-defined function which is to be executed
every time after
an optics calculation is done in CALCULATE(CAL) or GO commands. In GO, OpticsEpilog is cal
led at
the end of each iteration. This function is useful, for instance, for setting parameters w
hich depends
on the result of optics calculation itself.
See also:
OpticsProlog
-
OpticsProlog is a variable to assign a user-defined function which is to be executed
every time before
an optics calculation is done in the CALCULATE(CAL) or GO commands. In GO, OpticsProlog is
called
at the beginning of each iteration. This function is useful, for instance, for setting par
ameters
which depends on the result of optics calculation itself.
See also:
OpticsEpilog
-
PBUNCH is the number of particles/bunch for the calculation of the intra-beam and spa
ce charge effects
in EMITTANCE(EMIT), and WakeFunction. Accessible in MAIN.
See also:
EMITTANCE(EMIT) INTRA WSPAC WakeFunction
-
When PHOTONS is ON (default is OFF), TrackParticles generates a list of all photons r
adiated through
the tracking. The list is assigned to a symbol PhotonList. PhotonList is a list of
{en, gx, gy, gz, nx, ny, nz, xi1, xi2, xi3, np, nele}
where
en: photon energy [eV]
gx: GX coordinate of the emission point [m]
gy: GY coordinate of the emission point [m]
gz: GZ coordinate of the emission point [m]
nx: GX component of the photon direction vector
ny: GY component of the photon direction vector
nz: GZ component of the photon direction vector (nx^2+ny^2+nz^2)=1.
xi1: Stokes' parameter for polarization 45 degree to the GZ=0 plane.
xi2: Stokes' parameter for right-handed polarization
xi3: Stokes' parameter for polarization in the GZ=0 plane.
np: particle number
nele: component number in the beam line
The probability of each polarization is given by each Stokes' parameter as (1+xi)/2 . Trac
kParticles
always updates PhotonList. The length of PhtonList is the number of emitted photons.
Remember that the {GX, GY, GZ} = {0, 0, 0} and their directions are {z, -x, -y} at the
entrance
of the beam line by default. It is changeable by the GEO command anyway.
See also:
PHOTONS TrackParticles
-
The equilibrium RF phase (in radian, = 2 Pi EFFRFFREQ DTSYNCH/c) where the synchrotro
n radiation
loss and acceleration balances. If there are phase, voltage, frequency variations in RF ca
vities,
it is calculated based on "effective voltage". Effective with RING only.
See also:
EFFVC EFFRFFREQ DTSYNCH CAVI MULT
-
SIGE is the equilibrium momentum spread at the entrance of the beam line calculated
by EMIT/Emittance[SaveEMIT->True].
See also:
EMITX EMITY EMITZ SIGZ EMITTANCE(EMIT) Emittance
-
SIGZ is the equilibrium bunch length at the entrance of the beam line calculated by
EMIT/Emittance[SaveEMIT->True].
See also:
EMITX EMITY EMITZ SIGE EMITTANCE(EMIT) Emittance
-
SpeedOfLight is 299792458.
-
Number of unstable planes in the optics calculations. Equal to zero if all x and y op
tics are stable
for on/off-momentum and finite amplitude matching.
See also:
NetResidual MatchingResidual
-
STACKSIZ has the size of the stack for SADScript interpreter. It can be set by user a
t the MAIN level,
right before the first FFS session. The default value is 200000.
-
TITLE is a character-string to make the title of the plot in DRAW or GEO commands.
See also:
CASE DRAW GEO
Usage: SAVE [element-pattern]
saves the values of the elements. What are saved are the value of the default keyword of a
ll elements,
the values of the non-default keywords which have been changed manually or by the matching
. If ALL
is given it resets all keywords. If element-pattern is given, it is only limited to the el
ements
which match the pattern, otherwise all elements are saved.
See also:
RESET USE VISIT BYE STOP QUIT wildcards
The SEED command is obsolete. Use SeedRandom[] function instead of SEED.
See also:
MEASURE(MEA) machine-errors FIXSEED MOVESEED SeedRandom
SHOW prints out the current matching conditions.
FFS["SHOW"] or FFS$SHOW[] returns the current matching conditions as a list. Each eleme
nt has
a form of
{component1, component2, function, goal-value, number-of-momentums, scale},
which corresponds to the format of the print-out by SHOW.
See also:
matching-function-commands FIT FFS FFS$SHOW
Usage: SPLIT component length
splits the component into two pieces at the point where the distance from the entrance is
length.
The new components have the same name as the original, and the strengths are proportional
to the
new lengths. Only magnets and cavities can be split. You should CALCULATE(CAL) after SPLIT
to get
optical parameters after SPLIT. Matching using SPLIT element as a variable may degrade the
speed
of convergence.
STAT shows the current settings of flags, fit points,
special-variables, the region for DISPLAY, seed of the random number generator, and elapse
d CPU time,
etc.
See also:
special-variables flags
Exits FFS and returns to SAD/MAIN level, with saving the values of the elements.
See also:
QUIT SAVE ABORT USE VISIT BYE
TERM [INPUT(IN)] suspends the current input stream and switches it to the previous
input stream.
TERM OUTPUT(OUT) suspends the current output and switches it to the previous output stre
am.
See also:
CLOSE(CLO) INPUT(IN) READ OUTPUT(OUT) APPEND(APP) END
Usage: TYPE [element-pattern [element-pattern1..]]
prints out the values of elements which match element-pattern in the SAD MAIN input format
. Keywords
which have zero values are omitted unless it is the default variable. If non element-patte
rn is given,
all elements are printed out.
See also:
DISPLAY(DISP) VARIABLES(VAR) elements
Usage: REP [n] body UNTIL [expr1]
executes commands in body n times until expr1 gives nonzero. The number n can be any expre
ssion which
gives a number. If n is omitted, infinity is assumed. If expr1 is omitted, False(==0) is a
ssumed.
See also:
REPEAT(REP) expression command-syntax functions Do
Usage: USE [[NO]EXPAND] beam-line
switches the beam line used in FFS to the beam line given by beam-line. beam-line can be a
n BeamLine
object or the name of a beam line defined in MAIN. All information specific to the current
beam line,
such as matching conditions is lost. If the keyword EXPAND is given (default), the new bea
m line
is expanded, i.e., the values of components are refreshed to the saved values.
If a BeamLine object is used by USE or VISIT, the new beam line becomes a
new LINE in the MAIN level, with a name which is created automatically.
See also:
VISIT BYE EXPAND BeamLine BeamLineName
VARIABLES displays a list of current matching-variables and their present, previous,
saved, minimum,
and maximum values together with the COUPLEd master elements and their coefficients.
When executed in the FFS function, it returns the result as a list.
Usage: FFS["VAR"]
returns a list of nvar elements, where nvar is the number of current matching-variables gi
ven by
the FREE command. Each element has the form
{name, keyword, present, previous, saved, minimum, maximum, coupled-master-element, coup
ling-coefficient}
,
which corresponds to the output of the VARIABLES(VAR) command.
See also:
FREE COUPLE(COUP) FFS
Usage: VARY keyword element-pattern
changes the default-keyword of the elements which match element-pattern to keyword.
See also:
FREE elements wildcards
Usage: VISIT [[NO]EXPAND] beam-line
switches the beam line used in FFS to the beam line given by beam-line. beam-line can be a
n BeamLine
object or the name of a beam line defined in MAIN. All information specific to the current
beam line,
such as matching conditions are reserved, and the previous beam line is restored when BYE
command
is issued. If the keyword EXPAND is given (default), the new beam line is expanded, i.e.,
the values
of components are refreshed to the saved values.
If a BeamLine object is used by USE or VISIT, the new beam line becomes a new LINE in t
he MAIN
level, with a name which is created automatically.
See also:
USE BYE EXPAND BeamLine BeamLineName
Many commands and functions accept the wildcards as a specification for the name o
f elements or
components. The valid wildcards are:
* matches any zero or more characters.
% matches one character.
{..} matches any character enclosed.
{^..} matches any character not enclosed.
..|.. alternative pattern.
See also:
elements components DISPLAY(DISP) TYPE(T) SAVE RESET FREE FIX machine-errors ATTRIBUTE(ATTR) REJECT(REJ)
CALCULATE(CAL) functions Element LINE Twiss
