Python 入門講座 第7回: タイトル募集中¶
今日の目標
ファイルから読み込んだデータからグラフを作成します。 pandas, matplotlib モジュールなどを使います。
- csvファイルの読み込み
- pandas.read_csv関数
- pandas dataframe オブジェクト
- plot メソッド
- numpy ndarray オブジェクト
- matplotlib, pyplot
使用するデータについて¶
今日使用するデータは、人間の視細胞の感度曲線のデータです。
人間の視細胞には、暗所で主に働く高感度の桿体細胞と 明所で主に働く*錐体細胞があります。錐体細胞はさらに三種に分けられ、異なる三つの波長(L,M,S)を中心とした 感度特性を持っています。今回使うのはこの錐体細胞の感度曲線データです。
ここでは、 "Golz, J. & MacLeod, D. I. A. (2003). Colorimetry for CRT displays. Journal of the Optical Society of America A, 20, 769-781. " で公開されている錐体細胞の感度データの一つ(https://www.uni-kiel.de/psychologie/golz/publications/2003a/LMS_SMJ_2.dat) を使います。
このデータは、単色光に対する3種類の錐体細胞の応答を示しています。 各行には波長、3種の錐体細胞(L,M,S)の応答値がTAB('\t')を区切り文字として記録されています。 波長は可視範囲とされる 380nm ~ 780 nm の 1nm毎のデータが入っています。
"https://www.uni-kiel.de/psychologie/golz/publications/2003a/LMS_SMJ_2.dat" の中身
380 1.3813908E-05 5.7853991E-06 1.0858872E-03
381 1.8467576E-05 7.7568882E-06 1.4526153E-03
382 2.4600486E-05 1.0364576E-05 1.9356954E-03
383 3.2630763E-05 1.3792566E-05 2.5679468E-03
384 4.3069506E-05 1.8267868E-05 3.3895325E-03
...このような形式のファイルは広い意味でCSV(comma separated values)形式のファイルと呼ばれています。 この形式のファイルをPythonで取り扱うには、いくつかの方法がありますが、ここではpandas(python Data Analysis Library) モジュールを使います。 pandasモジュールは標準ライブラリではありませんが、広く使われています。pandas モジュールは、
python3 -m pip install pandas
などでインストールします。 matplotlibも
python3 -m pip install matplotlib
などでインストールできます。
CSVファイルを読み込む: pandasを使ってみる。¶
まず、 import文を使ってpandasをインポートしておきます。
import pandas,matplotlib,numpy, matplotlib.pyplot as pyplot
次に pandasのread_csv関数を使って csv形式のファイルを読み込みます。
pandasにはread_excel,read_json,read_html ファイルもあり、excelファイルなども簡単に取り扱うことが可能です。 pandasのread_csvはファイルだけでなく、
URIを与えることでweb上で公開されているデータファイルも直接取り扱うことができます。
LMS_URL="https://www.uni-kiel.de/psychologie/golz/publications/2003a/LMS_SMJ_2.dat"
df=pandas.read_csv(LMS_URL,
# sep="\s+", # 正規表現 \s:空白文字[\t\r\n\f], +:1以上の繰り返し
sep="\t",
header=None,
names=("wl","L","M","S"))
ターゲットのファイルは
- データ区切りとして、コンマ(
,)の代わりにTAB(\t)を使う。 ->sep="\t" - ヘッダ行はない ->
header=None - 納められているデータは単色光の波長("w"), 三つの錐体(L,M, S)の応答 ->
names=("wl","L","M","S")
という条件に従っていますので、これらの条件をread_csvの引数に与えます。
Pandas dataframe¶
読み込まれたデータはpandasのデータフレームと呼ばれるデータ形式になっています。
type(df)
pandas.core.frame.DataFrame
まずは最初の五つのデータを見てみましょう。
df[:5]
| wl | L | M | S | |
|---|---|---|---|---|
| 0 | 380 | 0.000014 | 0.000006 | 0.001086 |
| 1 | 381 | 0.000018 | 0.000008 | 0.001453 |
| 2 | 382 | 0.000025 | 0.000010 | 0.001936 |
| 3 | 383 | 0.000033 | 0.000014 | 0.002568 |
| 4 | 384 | 0.000043 | 0.000018 | 0.003390 |
データフレームは2次元の表データフレームはこの様に、行および列にそれぞれラベル(indexおよび column names)を持つ2次元の表として表現されます。¶
Excelの表や、RDB(Relationa DataBase)のテーブルを思い浮かべても良いでしょう。
| wl | L | M | S | |
|---|---|---|---|---|
| 0 | 380 | 0.000014 | 0.000006 | 0.001086 |
| 1 | 381 | 0.000018 | 0.000008 | 0.001453 |
| 2 | 382 | 0.000025 | 0.000010 | 0.001936 |
| 3 | 383 | 0.000033 | 0.000014 | 0.002568 |
| 4 | 384 | 0.000043 | 0.000018 | 0.003390 |
df.index, df.columns
(RangeIndex(start=0, stop=401, step=1), Index(['wl', 'L', 'M', 'S'], dtype='object'))
データフレームの成分の取り出し¶
データフレームはリストと同じ様にその成分を取り出すことができますが、より柔軟な方法で データと取り出すことができます。
- 行の範囲を指定してとりだす。
print(f"{df[0:3:1] = :}\n")
df[0:3:1] = wl L M S 0 380 0.000014 0.000006 0.001086 1 381 0.000018 0.000008 0.001453 2 382 0.000025 0.000010 0.001936
- 列を指定してとりだす。
print(f" {df.L[0]= },\t\t {df['M'][0]= }")
df.L[0]= 1.3813908e-05, df['M'][0]= 5.7853991e-06
- アクセス関数(
.loc,.atなど)を利用して成分を取り出す。
print(f"{df.loc[0]= },\n\n{df.at[0,'S']= }")
df.loc[0]= wl 380.000000 L 0.000014 M 0.000006 S 0.001086 Name: 0, dtype: float64, df.at[0,'S']= 0.0010858872
# ラベルを日本語にするために、fontを変更
font = {'family' : u'IPAGothic'}
matplotlib.rc('font', **font)
ax=df.plot.line("wl",["L","M","S"],
title=u"錐体の応答(LMS刺激値)",
xlabel="波長 [nm]",
ylabel=u"応答",
color=["r","g","b"],
legend=True,
)
.plot.line関数の返す値(ax)は、matplotlibのaxesオブジェクトとなっています。
pandasのグラフ機能は基本的にmatplotlibモジュールの機能を利用しています。
type(ax)
matplotlib.axes._subplots.AxesSubplot
このaxesオブジェクトを直接操作することで、グラフの一部を書き換えることも可能です。
ax.set_xlabel(u"波長 [nm]", family=u'IPAGothic')
ax.set_ylabel(u"視細胞の応答", family=u'Noto Sans Japanese')
ax.set_title(u"錐体の応答 (LMS刺激値)", family=u'IPAGothic')
pyplot.draw()
ax.figure
<Figure size 432x288 with 0 Axes>
プロットオプション:サブプロット¶
.plot関数のオプションを使うことで、様々なグラフを作りだすことができます。
axes=df.plot('wl',['L','M','S'],
kind='line', subplots=True,
title="LMS 刺激値",
xlabel="波長[nm]",
ylabel=u"応答",
color=["r","g","b"],
)
プロットオプション: 対数表示¶
#logscale
axl=df.plot.line("wl",["L","M","S"],
title="LMS 刺激値",
xlabel="波長[nm]",
ylabel=u"応答",
figsize=(6,5.5),
logy=True,
color=("r","g","b"),
ylim=(1e-3,None)
)
ax.figure.savefig("./_images/LMS.png")
保存したグラフの表示¶
matplotlib.pyplotモジュールのimreadとimshow関数を組み合わせることで、画像ファイルの
内容を表示することも簡単です。
pyplot.imshow(pyplot.imread("./_images/LMS.png"));
3原色表示¶
我々の色覚はこのように3種類の錐体細胞の応答値の組み合わせの違いを色として認識していると 考えられます。従って、3種類の光源を使い適切な組み合わせで混合することで、我々が 認識する色彩を再現することが可能となります。これは写真、ビデオ信号などの基礎となっています。 ISOの色彩に関する規格ではこの3種の光源として次の波長の光を基準としています。
# 光の3原色(RGB)
lambda_R=700 # in nm
lambda_G=546.1
lambda_B=435.8
マーカーの追加¶
先ほどのLMS応答グラフにこれら3原色の波長をしめすマーカーをつけてみます。
ymin,ymax=ax.get_ylim()
ax.arrow(lambda_R,-0.1, 0,0,
width=0.1,head_width=10, head_length=0.05,
color="red",head_starts_at_zero=False)
ax.arrow(lambda_G,-0.1, 0,0 ,
width=0.1,head_width=10, head_length=0.05,
color="green",head_starts_at_zero=False)
ax.arrow(lambda_B,-0.1, 0,0,
width=0.1,head_width=10, head_length=0.05,
color="blue",head_starts_at_zero=False)
ax.figure
アノテーションの追加¶
アノテーションを追加することでも、同様のマーカーを追加できます。
ax.annotate("R",(lambda_R, -0.1),
(0,-24),textcoords="offset points",color="red",fontsize=16,
arrowprops=dict(facecolor='red', shrink=0.05),
horizontalalignment='right', verticalalignment='top'
)
ax.annotate("G",(lambda_G, -0.1),
(0,-24),textcoords="offset points",color="green",fontsize=16,
arrowprops=dict(facecolor='green', shrink=0.05),
horizontalalignment='right', verticalalignment='top'
)
ax.annotate("B",(lambda_B, -0.1),
(0,-24), textcoords="offset points",color="blue",fontsize=16,
arrowprops=dict(facecolor='blue', shrink=0.05),
horizontalalignment='right', verticalalignment='top'
)
ax.figure
matplotlibとnumpy ndarray¶
この様に、pandasとそのデータフレームを使うことで、グラフを簡単に作成することができます。
しかし、そのグラフをより見易いものにするためには、ベースとなっているmatplotlibの理解と利用が必要となります。
matplotlibはpandasのみならず、Pythonの様々な数値処理モジュールなどで使われています。(つまりmatplotlibは
学んでおいて損はないということです。)
また、matplotlibを使いこなす上では、numpyの提供するndarrayが重要です。numpy ndarrayはmatplotlib同様に、様々な数値計算用 pythonモジュールの基礎として使われています。
matplotlib¶
matplotlibモジュールには、Figure,backend, Axes, Patches, Artists といったmatplotlibの基本となるオブジェクトやAPIなどへの玄関口です。
matplotlibモジュールを簡便につかえるように、matplotlib.pyplotモジュールが用意されています。このモジュールから使い始めるのが良いでしょう。
pylabモジュールは MATLAB に似たグラフ作成のためのAPIを提供しています。matplotlibモジュールはその名が示すように、MATLABのグラフ機能を意識して開発が始められました。しかし現在ではこのpylabモジュールの使用は公式ページで"推奨しない"とされています。
| matplotlibのオブジェクト |
|---|
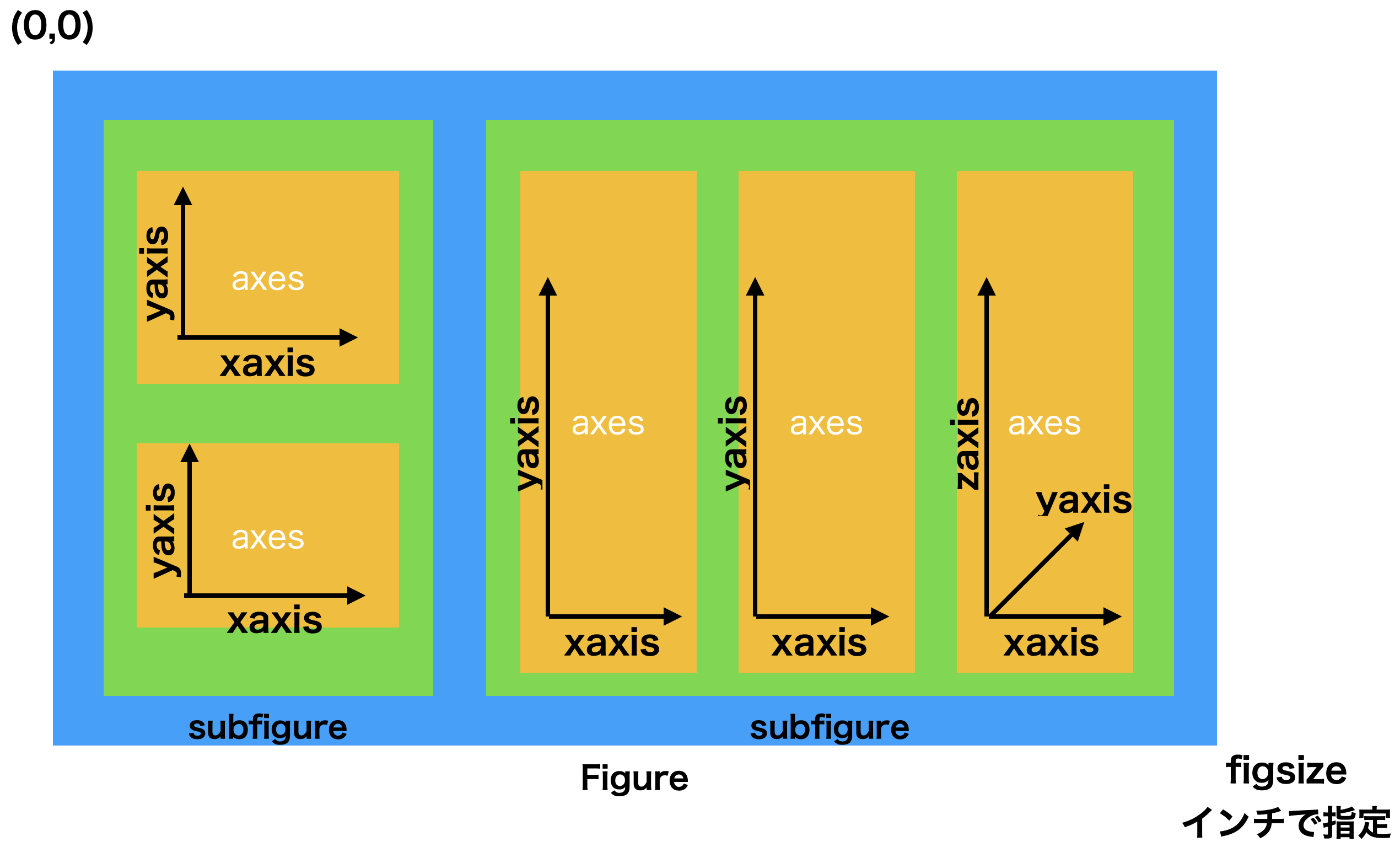 |
axesはfigure.add_subplot,figure.subplotsなどを使って生成する。
ndarray in numpy モジュール¶
pandasがグラフの生成にmatplotlibを使っているのと同様に、大量の数値の計算にはnumpyモジュールの機能を使っています。その中でも中心となるのは、ndarryオブジェクトです。
ndarrayは多次元のリストに似ていますが、一つのndarrayの基本要素は全て同じタイプを持っています。 (リストでは一つのリストに異なるタイプのオブジェクトが共存できます。) これにより、ndarrayでは多量の数値に対する計算が効率よく行えます。 (C/C++でいえば、pythonリストはObjectへのポインタの配列、ndarrayはオブジェクトそのものの配列ということになります。)
データフレームから ndarrayへ¶
データフレームの.valuesプロパティはデータフレームの内容をndarrayとして保持しています。
na= df.values; # also na=df.to_numpy()
type(na)
numpy.ndarray
ndarrayはリストとは異なり、全ての要素が同じデータ型(.dtype)をもっています。
na.dtype
dtype('float64')
shape¶
此の例では、作られたndarrayオブジェクトは401行4列の2次元の配列となっています。ndarrayは2次元以上の配列も実現できます。
na.shape
(401, 4)
na[:2,:] #最初の二行を表示
array([[3.8000000e+02, 1.3813908e-05, 5.7853991e-06, 1.0858872e-03],
[3.8100000e+02, 1.8467576e-05, 7.7568882e-06, 1.4526153e-03]])
shapeの変更¶
shapeは要素数が同じであれば、変更可能です。
na.shape=(401,2,2)
na[:2,:]
array([[[3.8000000e+02, 1.3813908e-05],
[5.7853991e-06, 1.0858872e-03]],
[[3.8100000e+02, 1.8467576e-05],
[7.7568882e-06, 1.4526153e-03]]])
ndarrayの要素の取り出し¶
ndarrayはリストとよく似た構造を持っていますが、 リストよりも柔軟な要素の取り出し方を持っています。
データフレームとは異なり、indexやcolumn namesは持っていません。リスト同様に行あるいは列の場所を示す番号とスライスで範囲を指定します。
na.shape=(401,4) # 元に戻す。
print(f"{na[-1,0] =:}\n") #最後の行の最初の列の要素
print(f"{na[0] =:}\n") # 最初の一行
print(f"{na[0:2] =:}\n") # 最初の2行
print(f"{na[0:2, :] =:}\n") # 最初の2行
print(f"{na[0:2,...] =:}\n") # 最初の2行
na[-1,0] =780.0 na[0] =[3.8000000e+02 1.3813908e-05 5.7853991e-06 1.0858872e-03] na[0:2] =[[3.8000000e+02 1.3813908e-05 5.7853991e-06 1.0858872e-03] [3.8100000e+02 1.8467576e-05 7.7568882e-06 1.4526153e-03]] na[0:2, :] =[[3.8000000e+02 1.3813908e-05 5.7853991e-06 1.0858872e-03] [3.8100000e+02 1.8467576e-05 7.7568882e-06 1.4526153e-03]] na[0:2,...] =[[3.8000000e+02 1.3813908e-05 5.7853991e-06 1.0858872e-03] [3.8100000e+02 1.8467576e-05 7.7568882e-06 1.4526153e-03]]
na[(0,200,400),...] #指定した行(0,200,400)をとりだす。
array([[3.8000000e+02, 1.3813908e-05, 5.7853991e-06, 1.0858872e-03],
[5.8000000e+02, 6.7649208e-01, 2.3602925e-01, 5.2250678e-04],
[7.8000000e+02, 1.4279820e-05, 6.3144453e-07, 1.3166252e-08]])
na[::200,...] # 200行毎にとりだす。ellipse(...)を使った。
array([[3.8000000e+02, 1.3813908e-05, 5.7853991e-06, 1.0858872e-03],
[5.8000000e+02, 6.7649208e-01, 2.3602925e-01, 5.2250678e-04],
[7.8000000e+02, 1.4279820e-05, 6.3144453e-07, 1.3166252e-08]])
na[::200,:] # 200行毎にとりだす。スライス(: )
array([[3.8000000e+02, 1.3813908e-05, 5.7853991e-06, 1.0858872e-03],
[5.8000000e+02, 6.7649208e-01, 2.3602925e-01, 5.2250678e-04],
[7.8000000e+02, 1.4279820e-05, 6.3144453e-07, 1.3166252e-08]])
na[slice(0,401,200),...] # 200行毎にとりだす。
array([[3.8000000e+02, 1.3813908e-05, 5.7853991e-06, 1.0858872e-03],
[5.8000000e+02, 6.7649208e-01, 2.3602925e-01, 5.2250678e-04],
[7.8000000e+02, 1.4279820e-05, 6.3144453e-07, 1.3166252e-08]])
pyplot モジュールによるグラフの作成¶
matplotlibのサブモジュールであるpyplotを使ってグラフを作成します。
import matplotlib.pyplot as pyplot
pyplot.ion()
pyplot.plot(na[:,0],na[:,1],"r", label="L")
pyplot.legend()
#pyplot.draw()
#pyplot.show()
<matplotlib.legend.Legend at 0x12a96f640>
複数のデータを含むグラフ¶
lines=pyplot.plot(na[:,0],na[:,1],"r",
na[:,0],na[:,2],"g",
na[:,0],na[:,3],"b")
pyplot.legend(["L","M","S"])
pyplot.xlabel("波長[nm]")
pyplot.ylabel("応答")
Text(0, 0.5, '応答')
タイトル ラベルの追加¶
fig=pyplot.figure(constrained_layout=False,figsize=(8,4)) # inches
ax=fig.add_subplot(1,1,1)
ax.plot(na[:,0],na[:,1],"r",label="L")
ax.plot(na[:,0],na[:,2],"g",label="M")
ax.plot(na[:,0],na[:,3],"b",label="S")
ax.set_title(u"三錐体(LMS)の応答")
ax.set_xlabel("波長[nm]", family="IPAGothic")
ax.set_ylabel(u"応答")
ax.set_xlim(None,None)
ax.legend()
<matplotlib.legend.Legend at 0x12aa9fd30>
サブプロット¶
fig=pyplot.figure(constrained_layout=True,figsize=(8,4))
axes=fig.subplots(3,1)
fig.suptitle("LMS 応答関数(個別)")
for i, ax, c, lbl in zip(range(1,4), axes, ["r","g","b"], ["L","M","S"]):
ax.plot(na[:,0],na[:,i],c,label=lbl)
ax.legend()
ax.set_ylabel("応答")
axes[-1].set_xlabel("波長[nm]")
pyplot.draw()
zip関数はジッパー(Zipper)が金具を互い違いに組み合わせて行く様に、複数のリストから要素を順次取り出して組み合わせてくれます。zip()はイテレータであるzipオブジェクトを返します。
>>> for p in zip([1,2,3],["a",'b',"c"]):
>>> print(p)
(1, 'a')
(2, 'b')
(3, 'c')
3D プロット¶
我々の色覚はこのように、3種の錐体細胞の刺激値の値の3次元空間内の一点として表現できます。 単色光の波長を変えたときのこの色空間のなかの軌跡を3次元グラフとして表現してみます。
ここでは、二つの3次元グラフの視点を少し変えることで立体視可能なグラフを試みてみました。
matplotlibでは、subplotを作る際にprojection="3d"を指定することで、
3次元のグラフが作成されます。
fig=pyplot.figure(figsize=(9,4), constrained_layout=True)
fig.suptitle("LMS curve in 3D");
zrot=2
axL=fig.add_subplot(1,2,1,projection='3d',
azim=-30-zrot,elev=30,proj_type='persp')
axR =fig.add_subplot(1,2,2,projection='3d',
azim=-30+zrot,elev=30,proj_type='persp',
sharez=axL,sharex=axL,sharey=axL)
def plotLMS3D(ax,na):
ax.set_xlabel('L')
ax.set_ylabel('M')
ax.set_zlabel('S')
L,M,S =na[:,1], na[:,2], na[:,3]
ax.plot(L,M,S,label="LMS")
plotLMS3D(axL,na);
plotLMS3D(axR,na);
axL.set_title("Left");
axR.set_title("Right");
LMSに変わり、輝度$Y = L+M+S$で正規化した色空間座標 $l=L/Y, m=M/Y, s=S/Y$で同じデータをプロットします。$ l+m+s=1$が成り立ちますから、この色空間では全ての色は一平面上に存在することになります。
fig=pyplot.figure(figsize=(9,4), constrained_layout=True)
fig.suptitle("lms curve in 3D");
zrot=2
axL=fig.add_subplot(1,2,1,projection='3d',
azim=-30-zrot,elev=30,proj_type='persp')
axR =fig.add_subplot(1,2,2,projection='3d',
azim=-30+zrot,elev=30,proj_type='persp',
sharez=axL,sharex=axL,sharey=axL)
def plotLMS3D(ax,na):
ax.set_xlabel('l') ; ax.set_ylabel('m'); ax.set_zlabel('s')
L,M,S =na[:,1], na[:,2], na[:,3]
Y=L+M+S
L,M,S=L/Y,M/Y,S/Y
ax.plot(L,M,S,label="lms")
plotLMS3D(axL,na);
plotLMS3D(axR,na);
axL.set_title("Left");
axR.set_title("Right");
pyplot.draw(), pyplot.show(), pyplot.ion(),pyplot.ioffについて¶
jupyterlabのNotebookなどでは不要ですが、端末などでpythonを起動して、matplotlibのグラフを表示する場合、
適切にpyplot.draw(), pyplot.show() を使う必要があります。(jupyterlab/ipythonなどの環境では、
jupyterlab/ipythonのシステムが良きに計らってくれます。)
matplotlibをpythonで使う際には、noninteractive modeとinteractive modeの違いを意識する必要があります。
non-interactiveモード(デフォールト)¶
matplotlibを起動した直後は non-interactiveモードになっています。pyplot.ion()でinteractiveモードに
移行できます。non-interactiveモードに戻るには
pyplot.draw()¶
plotなどのコマンドを実際のグラフに反映させるためには、pyplot.draw()を実行する必要があります。
pyplot.show()¶
Figureおよびその内容(つまりグラフです)はpyplot.show()を呼び出すことで、画面に表示されます。
画面が表示されている間は, キーボード/マウスはグラフ表示画面に結びつけられており、python処理系をキーボードから制御することはできません。
グラフを表示しているウィンドを閉じることで、python処理系に制御が戻ります。それまでに作成したグラフの情報は破棄されます. (Figure, Axesなどのオブジェクトが削除されます。)
interactiveモード¶
pyplot.ion()を実行することで、interactiveモードに移行します。
interactiveモードpyplot.plotなどのコマンドを実行すると、グラフ表示窓が作成され、その中のグラフが更新されます。グラフの更新のためにpyplot.draw(), pyplot.show()を使う必要はありません。pyplot.show()を呼ぶと、グラフ表示窓がアクティブになり、画面の全面に出てきます。
python処理系はプログラム入力状態にありますので、新たなプログラムを入力できます。グラフ表示窓のマウスによる操作も有効です。
interactiveモードでpython処理系を終了すると、グラフ表示窓も消去されます。
pyplot.ioff() で non-interactiveモードに戻ります。
jupyterlab Notebookの%matplotlib マジックについて¶
jupyterlabなどのNotebookでは%matplotlibマジックコマンドが用意されています。
jupyter
%matplotlib [-l/--list] [gui]-l/--listオプションでmatplotlibが使用するバックエンド処理系を選択できます。
inlineバックエンドを使うと、Notebookの中のグラフを操作することが出来るようになるとのことです。
(私のmacbook/jupyterlab環境ではうまく動作しないので、...)
%matplotlib --list
Available matplotlib backends: ['tk', 'gtk', 'gtk3', 'gtk4', 'wx', 'qt4', 'qt5', 'qt6', 'qt', 'osx', 'nbagg', 'notebook', 'agg', 'svg', 'pdf', 'ps', 'inline', 'ipympl', 'widget']
3原色の色覚曲線¶
先ほど述べたように、3種類の色の異なる光源を組み合わせることで、LMS色空間の任意の色を再現できることになります。 この加色法による色表現で、単色光の色を再現するために必要となる三原色の強度の組み合わせを求めてみます。 波長$\lambda$に対するこのRGBの各成分の強度の関数は等色関数と呼ばれます。
線形補間関数を作る。¶
LMSのテーブルは1 nm毎に与えられていますが、3原色の波長でのLMSの値を求めるためには、CIE/JIS規格に 従い
線形補間を行う必要があります。波長と刺激値のテーブルから、線形補間された刺激値を計算する関数を返す関数をここで定義します。
def lininterp(v):
w=[e[0] for e in v]
s=[e[1] for e in v]
def interp(x,_w=w,_s=s):
i=j=None
if int(x) in _w:
i=_w.index(int(x))
if int(x)+1 in _w:
j=_w.index(int(x)+1)
if i and j:
ret=(_s[i]*(_w[j]-x)+_s[j]*(x-_w[i]))/(_w[j]-_w[i])
return ret
elif i:
return _s[i]
elif j:
return _s[j]
else:
return 0
return interp
この(汎)関数を使って、波長$\lambda$での単色光に対する刺激値を求める関数 L,M,S を定義します。
lambda_R, lambda_G, lambda_B =700, 546.1,435.8
L_tbl ,M_tbl, S_tbl =[ na[:,[0,i]] for i in range(1,4)]
L,M,S=lininterp(L_tbl),lininterp(M_tbl),lininterp(S_tbl)
RGBからLMSへの変換¶
色覚では、応答の線形性が(少なくとも近似的には)成り立つことが経験的にしられています。 3原色の光を或る強度で混ぜ合わせたとき、錐体細胞が受け取る刺激値は、次の行列を使って求めることができます。
この行列の逆を求めることで、LMSの刺激値を再現するためのRGBの強度を求める係数行列を得ます。
mat_RGB_to_LMS=numpy.matrix((
(L(lambda_R), L(lambda_G), L(lambda_B)),
(M(lambda_R), M(lambda_G), M(lambda_B)),
(S(lambda_R), S(lambda_G), S(lambda_B))
))
mat_LMS_to_RGB=mat_RGB_to_LMS**(-1)
print(f"{mat_RGB_to_LMS = !r}\n\n{mat_LMS_to_RGB = !r}")
mat_RGB_to_LMS = matrix([[4.02808400e-03, 6.51276398e-01, 2.14291164e-02],
[1.41605110e-04, 3.63393490e-01, 1.85730100e-02],
[4.40129960e-07, 6.78473818e-03, 1.85053618e+00]])
mat_LMS_to_RGB = matrix([[ 2.64950902e+02, -4.74878594e+02, 1.69802741e+00],
[-1.03260691e-01, 2.93743062e+00, -2.82859332e-02],
[ 3.15575522e-04, -1.06567435e-02, 5.40487225e-01]])
mat_RGB_to_LMS と mat_LMS_to_RGB が違いに逆行列になっているこを確認してみましょう。
行列の積は色々な方法でpythonプログラム中で記述できます。numpy.matrixで定義した行列については、@を行列積のオペレータとして使うことができます。
print(f"{mat_LMS_to_RGB@mat_RGB_to_LMS = !r}\n\n{mat_RGB_to_LMS@mat_LMS_to_RGB = !r}")
mat_LMS_to_RGB@mat_RGB_to_LMS = matrix([[ 1.00000000e+00, 4.93528829e-14, 1.77635684e-15],
[-1.77347523e-20, 1.00000000e+00, -6.93889390e-18],
[-7.94093388e-23, 4.33680869e-19, 1.00000000e+00]])
mat_RGB_to_LMS@mat_LMS_to_RGB = matrix([[ 1.00000000e+00, 9.50845305e-17, 0.00000000e+00],
[ 7.46913653e-18, 1.00000000e+00, -1.73472348e-18],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
この変換行列mat_LMS_to_RGB を使って、単色光の色を再現するためのRGBの強度を求めてみます。
import numpy.linalg as linalg
LMS=na[:,1:]
print(f"{LMS.shape = }")
#LMS.shape=(LMS.shape[0],3,1)
print(LMS[0])
RGB=LMS@(mat_LMS_to_RGB.transpose())
print(RGB[0],RGB.shape)
LMS.shape = (401, 3) [1.3813908e-05 5.7853991e-06 1.0858872e-03] [[ 2.75651142e-03 -1.51475581e-05 5.86850866e-04]] (401, 3)
等色関数をプロットする。¶
RGBの各成分を波長を横軸にプロットしてみます。
fig=pyplot.figure()
ax=fig.add_subplot(1,1,1)
for i,c in enumerate(["r","g","b"]):
ax.plot(na[:,0],RGB[:,i],c,label=c.upper())
ax.legend()
<matplotlib.legend.Legend at 0x12ad2e7c0>
RのLMS感度がG,Bに比べて小さいためこの様なグラフになってしまいます。 RGBの強度のユニットを正規化することで、等色関数の最大値が1になる様に、正規化します。
fig=pyplot.figure()
ax=fig.add_subplot()
RGB_scale=[1/max(RGB[:,i]) for i in range(3)]
for i,c in enumerate(["r","g","b"]):
ax.plot(na[:,0], RGB[:,i]*RGB_scale[i], c,label=c.upper())
ax.legend()
<matplotlib.legend.Legend at 0x12ad62c40>
この形の等色曲線がよく資料などに使われています。
この等色曲線では一部で値が負の値になっています。この様な領域では、その波長の単色光をRGBの3原色では再現できないことを意味しています。
波長と刺激値を4次元ベクトルとして取り扱うことも可能です。
mat_wRGB_to_wLMS=numpy.matrix((
(1, 0, 0, 0),
(0, L(lambda_R), L(lambda_G), L(lambda_B)),
(0, M(lambda_R), M(lambda_G), M(lambda_B)),
(0, S(lambda_R), S(lambda_G), S(lambda_B))
))
mat_wLMS_to_wRGB=mat_wRGB_to_wLMS**(-1)
print(f"{mat_wRGB_to_wLMS = !r}\n\n{mat_wLMS_to_wRGB = !r}\n")
print(f"{mat_wLMS_to_wRGB@mat_wRGB_to_wLMS = !r}\n\n{mat_wRGB_to_wLMS@mat_wLMS_to_wRGB = !r}")
mat_wRGB_to_wLMS = matrix([[1.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[0.00000000e+00, 4.02808400e-03, 6.51276398e-01, 2.14291164e-02],
[0.00000000e+00, 1.41605110e-04, 3.63393490e-01, 1.85730100e-02],
[0.00000000e+00, 4.40129960e-07, 6.78473818e-03, 1.85053618e+00]])
mat_wLMS_to_wRGB = matrix([[ 1.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00],
[ 0.00000000e+00, 2.64950902e+02, -4.74878594e+02,
1.69802741e+00],
[ 0.00000000e+00, -1.03260691e-01, 2.93743062e+00,
-2.82859332e-02],
[ 0.00000000e+00, 3.15575522e-04, -1.06567435e-02,
5.40487225e-01]])
mat_wLMS_to_wRGB@mat_wRGB_to_wLMS = matrix([[ 1.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00],
[ 0.00000000e+00, 1.00000000e+00, 2.09311735e-14,
8.88178420e-16],
[ 0.00000000e+00, -1.77347523e-20, 1.00000000e+00,
-6.93889390e-18],
[ 0.00000000e+00, -7.94093388e-23, 4.33680869e-19,
1.00000000e+00]])
mat_wRGB_to_wLMS@mat_wLMS_to_wRGB = matrix([[ 1.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00],
[ 0.00000000e+00, 1.00000000e+00, 9.50845305e-17,
0.00000000e+00],
[ 0.00000000e+00, 5.30242625e-19, 1.00000000e+00,
-1.73472348e-18],
[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
1.00000000e+00]])
蛍光体のスペクトラム¶
これまで、R,G,Bの各色は単色光と仮定しましたが、実際の発光体は幅を持ったスペクトラムを持っています。 最初にご紹介した論文では、発光体のスペクトラムの一例も紹介されています。
av_phosphors=pandas.read_csv(
"https://www.uni-kiel.de/psychologie/golz/publications/2003a/AveragePhosphors.dat",
sep="\t",
header=None,
names=("wl","R","G","B")
)
この発光体のスペクトラムをグラフに表示してみましょう。¶
av_phosphors.plot.line("wl",["R","G","B"],color=["red","green","blue"])
<AxesSubplot:xlabel='wl'>
スペクトルの正規化¶
可視光領域でのスペクトルの総和が同じになるように、蛍光体のスペクトルを正規化します。
scale=numpy.diag( [1/av_phosphors.values[:,i].sum() for i in range(1,4)])
NRGB=av_phosphors.values[:,1:]@scale
RGB=av_phosphors.values[:,1:]
fig=pyplot.figure()
fig.suptitle("ディスプレィ蛍光体の平均発光スペクトラム\n正規化済み")
ax=fig.add_subplot(1,1,1)
ax.plot(av_phosphors["wl"],NRGB[:,0],"r",label="R")
ax.plot(av_phosphors["wl"],NRGB[:,1],"g",label="G")
ax.plot(av_phosphors["wl"],NRGB[:,2],"b",label="B")
ax.legend()
<matplotlib.legend.Legend at 0x12a92fc10>
import scipy.io, io, urllib.request
monitors=scipy.io.loadmat(
io.BytesIO(
urllib.request.urlopen(
"https://www.uni-kiel.de/psychologie/golz/publications/2003a/Phosphors.mat"
).read())
)["phosphors"]
monitors.shape
(401, 3, 15)
この発光体のスペクトラムをグラフに表示してみましょう。
fig=pyplot.figure(figsize=(12,6))
fig.suptitle("各種モニターでの蛍光体 発光特性", family=u'IPAMincho',fontsize=24)
axes=fig.subplots(3,5)
for i,ax in enumerate(axes.flatten()):
ax.plot(na[:,0], monitors[:,0,i],color="red",label="R")
ax.plot(na[:,0], monitors[:,1,i],color="green",label="G")
ax.plot(na[:,0], monitors[:,2,i],color="blue",label="B")
pyplot.draw()
今日のまとめ¶
ファイルから読み込んだデータからグラフを作成しました。 pandas, matplotlib モジュールなどを使いました。
- csvファイルの読み込み
- pandas.read_csv関数
- pandas dataframe オブジェクト
- plot メソッド
- numpy ndarray オブジェクト
- matplotlib, pyplot