5. 出発ゲート：一列にならんで、順番に¶
今回の話題:
リストとタブル 一列に並んだデータを保持するデータ型
mutableとimmutable
繰り返し(for文、 リスト内包表記、ジェネレーター式)
簡単なグラフの作成
(例外処理：入力値のチェック)
5.1. 数列を作ってみる。¶
前回はPythonで関数を定義する方法の基本を学びました。 今回は、実際に数値の値を返す関数を定義して見ます。
まずフィボナッチの数列を求める関数を定義してみましょう。
5.2. フィボナッチ数列とは？¶
フィボナッチ数列([1, 1, 2, 3, 5, 8, 13, 21,…])とは
\(a_0 = 1\)
\(a_1 = 1\)
\(a_n = a_{n-1} + a_{n-2} \qquad \text{ ( for}\ n \gt 1 \text{ )}\)
で定義される数列です。
漸化式を解いて、
\(a_=\frac{1}{\sqrt 5}\left\lbrace(\frac{1+\sqrt 5}{2})^{n+1} - (\frac{1-\sqrt 5}{2})^{n+1}\right\rbrace\)
と定義することも可能です。
## 関数としての数列 整数\(n\)に対してフィボナッチの数列の\(n\)番目の数、\(a_n\)は一意に定りますから、これを関数と考えることもできます。
\(fib: n \mapsto a_n\)
漸化式を直接使って、Pythonでこの数列を関数として表現して見ます。
def fib(n:int)->int:
"""
フィボナッチ数列の n番目(n:= 0,1,2,..)の値を求める。
例：
>>> fib(2)
2
>>> fib(5)
8
"""
if n == 0 or n == 1:
value= 1
else:
value= fib(n-1) + fib(n-2)
return value
returnは関数の呼び出し元に、関数の結果を送りだします。ここでは変数valueの数値を返しています。Pythonでは、数値だけではなく様々なデータを返すことが可能です。
5.3. helpメッセージ¶
fibの定義にはdocstringが含まれています。
これにより、この関数の使い方などを確認することができます。
help(fib)
Help on function fib in module __main__:
fib(n: int) -> int
フィボナッチ数列の n番目(n:= 0,1,2,..)の値を求める。
例：
>>> fib(2)
2
>>> fib(5)
8
ここで、定義した関数 fib(n)
が、正しくフィボナッチの数列を求めているかどうかを確かめて見ましょう。
fib(0), fib(1), fib(2), fib(3), fib(4), fib(5),
(1, 1, 2, 3, 5, 8)
とフィボナッチ数が計算されていることが確認できました。
5.4. 繰り返し： for文¶
さきほどは、fib関数の動作確認のために、fib(0),...などを書き並べました。
しかし、いちいち引数の値を書くのは大変です。
for文を使えば異なる引数の値に対して、関数の値を求めることも簡単です。
for i in range(0,10,1):
print("fib(",i,")=",fib(i), end=", ")
print("...")
fib( 0 )= 1, fib( 1 )= 1, fib( 2 )= 2, fib( 3 )= 3, fib( 4 )= 5, fib( 5 )= 8, fib( 6 )= 13, fib( 7 )= 21, fib( 8 )= 34, fib( 9 )= 55, ...
printで フォーマット文字列を使った例。次回の講座で説明します。
for i in range(0,10,1):
print(f"fib({i}) = {fib(i)}", end=", ")
print("...")
fib(0) = 1, fib(1) = 1, fib(2) = 2, fib(3) = 3, fib(4) = 5, fib(5) = 8, fib(6) = 13, fib(7) = 21, fib(8) = 34, fib(9) = 55, ...
5.4.1. for文¶
for文は
for <識別子> in <リストやタプルなどのオブジェクト:iterable> :
<プログラム文>
...
の形をしています。この文を実行すると、<リスト、タプル、などのオブジェクト>の要素毎に、その値が<識別子>に割り当てられて、:の後に続く <プログラム文> が実行されます。
for i in range(0,10,1):
print("fib(",i,")=", fib(i), end=", ")
print("...")
fib( 0 )= 1, fib( 1 )= 1, fib( 2 )= 2, fib( 3 )= 3, fib( 4 )= 5, fib( 5 )= 8, fib( 6 )= 13, fib( 7 )= 21, fib( 8 )= 34, fib( 9 )= 55, ...
この繰り返しの中で、iは
0から始まり、i < 10の範囲で1ずつ増えていることがわかります。
list()関数を使うことで明示的に値の範囲を確認できます。
range(0,10,1)は0から始まって、10以下の、1づつ増える整数の列を表現しています。
list(range(0, 10, 1))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
注：
正確に言えば、list()は listクラスの生成子です。が、いまはデータ型を変換する関数と考えても、結果は同じです。
同様にrange(0,10,1)はrangeクラスの生成子を使っていることになります。
type(range(0, 10, 1))
range
5.5. リストとタプル(tuple)¶
for文を使うことで、 一連の\(n\)の値に対して、フィボナッチ数列の値を求めることができました。 せっかく計算したこれらの結果を印刷するだけでなく、データとして再利用できれば便利です。
こうした一連のデータをまとめて表現するために、Pythonにはリスト と
タブル
という2種類の一列に並んだデータを表現するデータ型が用意されています。
5.5.1. リスト(list)¶
1から5までの整数に対するフィボナッチ数列の値を要素に持つリストは次のようにして、作ることができます。
list_of_fib=[ fib(0),fib(1),fib(2),fib(3),fib(4),fib(5) ]
print(list_of_fib)
[1, 1, 2, 3, 5, 8]
5.5.2. タプル(tuple)¶
一方、1から5までの整数に対するフィボナッチ数列の値を要素に持つタプルは次のように作ることができます。
tuple_of_fib=( fib(0),fib(1),fib(2),fib(3),fib(4),fib(5) )
print(tuple_of_fib)
(1, 1, 2, 3, 5, 8)
このように、リストは[]で囲まれたデータの並び、タプルは()で囲まれたデータの並びとして表現されます。
リストやタプルは、for文での変数の範囲を指定するために使うことができます。
for i in list_of_fib:
print(i, end=", ")
1, 1, 2, 3, 5, 8,
5.5.3. リテラル定数としてのリストとタプル¶
リスト:記号[と]でリストの要素を,で区切って並べる。 ([1,2,3]と[1,2,3,]は同じ意味)タブル:記号(と)でリストの要素を,で区切って並べる。((1,2,3)と(1,2,3,)は同じ意味)[]は空のリスト(要素数が0）を表す。()は空のタプル（要素数が0）を表す。要素数が1のタプルは ``(1,)``と書く必要がある。 [
（1）は 数式と解釈されるため]
[1]==[1,], (1)==(1,)
(True, False)
5.5.4. 要素の取り出し。¶
リストやタプルの要素を取り出すことができます。
最初の要素は、
S[0]最後の要素は、
S[-1]\(n+1\)番目の要素は
S[n]\(n+1\)番目から\(m+1\)番目までの要素は
S[n:m]\(n+1\)番目から最後の要素までは
S[n:]\(n+1\)番目から\(m+1\)番目まで,\(l\) 置きの要素は
S[n:m:l]
5.5.5. list/tupleと要素指定¶
pythonでは指標（インデックス）は要素と要素の間を指していると考えると、理解しやすいでしょう。
図-5.1 Pythonでのリスト／タプルの要素とインデックスの関係¶
list_of_fib[:-8:-1]
[8, 5, 3, 2, 1, 1]
list_of_fib
[1, 1, 2, 3, 5, 8]
list_of_fib[0:-1:2]
[1, 2, 5]
0:-1:2はpythonではスライスと呼ばれます。
図-5.2 Pythonでのリスト／タプルの要素とスライス¶
print([list_of_fib[0], list_of_fib[4]], (tuple_of_fib[0],tuple_of_fib[4]))
print(list_of_fib[2:5], tuple_of_fib[2:5])
print(list_of_fib[0:-1:2], tuple_of_fib[0:-1:2])
[1, 5] (1, 5)
[2, 3, 5] (2, 3, 5)
[1, 2, 5] (1, 2, 5)
print([list_of_fib[0], list_of_fib[4]], (tuple_of_fib[0],tuple_of_fib[4]))
print(list_of_fib[2:5], tuple_of_fib[2:5])
print(list_of_fib[0:-1:2], tuple_of_fib[0:-1:2])
[1, 5] (1, 5)
[2, 3, 5] (2, 3, 5)
[1, 2, 5] (1, 2, 5)
s= slice(0,-1,2)
list_of_fib[s]
[1, 2, 5]
5.5.6. 変更可能か変更不可能か、それが問題 :リストとタプルの使い分け¶
- リストもタプルも n番目(nは0始まり）の要素を [n]を変数名(オブジェクト）に追加することで取り出すことができます。
ところが
リストは要素を更新することができる。(mutable)
タプルは要素を変更することができない。(immutable)
という大きな違いがあります。
リストの最初の要素(0番の要素）を置き換えてみます。
try:
list_of_fib[0]=2; print("list:", list_of_fib)
except TypeError as err:
print("TypeError:",err)
list: [2, 1, 2, 3, 5, 8]
tupleの要素を置き換えようとすると、…
try:
tuple_of_fib[0]=2; print("tuple:", tuple_of_fib)
except TypeError as err:
print("TypeError:",err)
TypeError: 'tuple' object does not support item assignment
list_of_fib[0]=2; print("list:", list_of_fib)
try:
tuple_of_fib[0]=2; print("tuple:", tuple_of_fib)
except TypeError as err:
print("TypeError:",err)
list: [2, 1, 2, 3, 5, 8]
TypeError: 'tuple' object does not support item assignment
というように、リストの要素を置き換えることはできますが、タプルの要素を置き換えることは例外を発生してしまいます。
リストへの要素の追加¶
リストに要素を追加する(append)ことはできますが、タプルに要素を追加することはできません。
#リストへの要素の追加 append
print("追加前：", id(list_of_fib), list_of_fib )
list_of_fib.append(fib(len(list_of_fib)))
print("追加後：", id(list_of_fib), list_of_fib)
追加前： 140429335990976 [2, 1, 2, 3, 5, 8]
追加後： 140429335990976 [2, 1, 2, 3, 5, 8, 13]
要素の追加前後で、リストの idが変わっていないことに注意してください。
# タプルへの要素の追加
print("追加前：",id(tuple_of_fib), tuple_of_fib)
try:
tuple_of_fib.append(fib(len(tuple_of_fib)))
print("追加後：", id(tuple_of_fib), tuple_of_fib)
except AttributeError as err:
print("AttributeError:", err)
tuple_of_fib=tuple_of_fib + (fib(len(tuple_of_fib)),)
print("追加後：",id(tuple_of_fib), tuple_of_fib)
追加前： 140429336116960 (1, 1, 2, 3, 5, 8)
AttributeError: 'tuple' object has no attribute 'append'
追加後： 140429336116864 (1, 1, 2, 3, 5, 8, 13)
タプルへ直接要素を追加することはできません。 タプルに新しい要素を付け加えたタプルを作り直して、変数に割り当て直すことは可能です。
5.6. ジェネレーター式(Generator expression)とリスト内包表記(List comprehension)¶
フィボナッチ数列の最初の10項を成分にもつリストはリスト内包表記を使うと、次のようにして つくることができます。
# リスト内包表記（list comprehension
[fib(i) for i in range(10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
ジェネレーター式はリスト内包表記に似た形ですが、()で囲われています。(リスト内包表記は[])
ジェネレーター式の値のオブジェクトは、next()で呼ばれるたびに、次の要素を値として返します。
[参考:
このように、next()の呼び出しに対して、次々と値を返すオブジェクトをiteratorと呼びます。]
g=(fib(i) for i in range(10))
print (type(g))
print(next(g), next(g), next(g), next(g), next(g), next(g))
<class 'generator'>
1 1 2 3 5 8
ジェネレーター式はfor()文で変数の範囲を示すために利用できます。
g=(fib(i) for i in range(10))
for i in g:
print(i,end=", ")
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
ジェネレーター式とリスト内包表記の一般形
# Generator expression -- returns iterator
stripped_iter = (line.strip() for line in line_list)
# List comprehension -- returns list
stripped_list = [line.strip() for line in line_list]
print([fib(i) for i in range(6)])
[1, 1, 2, 3, 5, 8]
ジェネレーター式はmap関数とほぼ等価。
ジェネレーター式をつかえるようになってmapの出番はなくなりました。
# mapとリスト内包表記
map(fib, range(10)), list(map(fib, range(10)))
(<map at 0x7fb860296790>, [1, 1, 2, 3, 5, 8, 13, 21, 34, 55])
[x for x in map(fib,range(10))]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
for x in (fib(i) for i in range(10)):
print (x, end=", ")
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
# generatorを使ってみる。
g=((fib(i) for i in range(10)))
try:
while(x:=next(g)): # walrus 式
print(x, end=" ")
except StopIteration:
print()
1 1 2 3 5 8 13 21 34 55
5.7. Pythonに組み込みのデータ型¶
pythonのリストおよびタプルというデータ型を紹介しました。
ここで、pythonに組み込みのデータ型を挙げて見ます。今回取り上げないデータ型は後ほど取り上げてい行きます。
Pythonではさらにclass文を使い、 新しいデータ型を定義することができます。 ブジェクト志向プログラム（OOP:Object
Oriented Program)で使われます。
5.7.1. 数¶
整数型
整数 （
int) ：明示的な桁数の制限はない(実行時にメモリが確保できる限りの桁数）論理定数型 (
bool) :TrueとFalse
浮動小数点数 (\(\ne\)実数) (
float) : 倍精度浮動小数点数 （4倍精度浮動小数点などにはnumpyなどのライブラリを使う。）複素数 (
complex)
5.7.2. コンテナ(データの集まり）¶
シークェンス型: immutable
タプル型 (
tuple)文字列型 (
str) : Pythonでは単独の文字というデータ型はありません。文字は1文字でも文字列型(次項参照）のデータとなります。バイト型 (
bytes) :
シークェンス型: mutable
リスト型 (
list)バイト配列型( bytearray )
集合 -集合型 (
set） : mutableなオブジェクトは要素になれない。 例: { 1,2,3 ,“a”,“b”,“c”} -不変な集合型 （frozenset): immutable & hashable辞書型 （
dict) :keyとvalueの組みをもつ。keyによる検索が可能。 例： {‘a’:1,‘b’:2,}
5.7.3. プログラムの実行に係るデータ型¶
ユーザ定義関数 ( function ) : 関数定義文で生成される関数オブジェクト
クラス (
class) ：class文によって生成される。モジュール( module )
その他 ….
5.8. グラフを描いてみます。¶
数字が一列に並んだものがあると、グラフにして見なくなるのは、物理研究者の（？ ）習い性です。
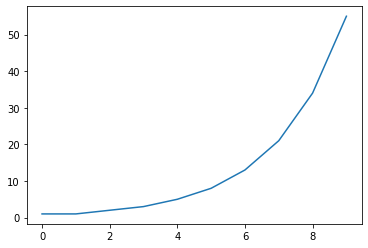
matplotlibライブラリの中のpyplotモジュールを使って、フィボナッチ数列のグラフを描いてみます。
import matplotlib.pyplot as pyplot
x=range(10)
pyplot.plot(x,[fib(n) for n in x])
pyplot.savefig("./_images/fibonacci.png")
pyplot.show()
6. エラーの処理：例外(Exception)の送出と受信¶
フィボナッチ数列 \(a_n\) は整数 \(n\) について定義されています。
では、ここで定義した関数 fib(n)のnに整数でない数値をあたえると何が起きるでしょう？
一例としてfib(1.1)を計算してみます。
fib(1.1)
---------------------------------------------------------------------------
RecursionError Traceback (most recent call last)
<ipython-input-37-6e83ab7f6d28> in <module>
----> 1 fib(1.1)
<ipython-input-1-efa726d55397> in fib(n)
11 value= 1
12 else:
---> 13 value= fib(n-1) + fib(n-2)
14 return value
... last 1 frames repeated, from the frame below ...
<ipython-input-1-efa726d55397> in fib(n)
11 value= 1
12 else:
---> 13 value= fib(n-1) + fib(n-2)
14 return value
RecursionError: maximum recursion depth exceeded in comparison
整数でない入力値nにたいしては停止条件n==0
あるいはn==1が決して満たされないため、システムの条件までプログラムはある意味暴走してしまいます。
このように、関数に与えられた引数が適切なものであるかを判断し、条件が満たされない場合には、そのことを関数の呼び出しもとにつたえるための仕組みとして、例外(Exception)の仕組みがpythonには用意されています。
入力値のチェックを組み込んだfib関数をご覧ください。
def fib(n:int)->int:
"""
return a value of fibonacci series for integer n.
>>> fib(10)
89
>>> fib(-1)
Traceback (most recent call last):
...
ValueError: n must be >= 0
>>> fib(1.0)
Traceback (most recent call last):
...
TypeError: n must be an exact integer
"""
if type(n) is not int:
raise TypeError("n must be an exact integer")
if not n >= 0:
raise ValueError("n must be >= 0")
if n == 0 or n == 1:
value = 1
else:
value= fib(n-1) + fib(n-2)
return value
この関数で実際にn=1.1のfib関数を計算して見ます。
fib(1.0)
このように、整数以外の数値が引数として与えられたことがエラーの原因であることがすぐにわかります。
この定義ではdocstringも入れてあるので、helpメッセージも表示されます。
help(fib)
さらに、docstringにはこの関数で予期される動作の例も書き込まれているので、
doctest
をつかって、この定義が設計を満たしているかどうかを確認することが
できます。
import doctest
doctest.testmod(verbose=True)
doctest.testmod(verbose=False)
n=8
try:
r=fib(n)
except TypeError as err:
print("TypeError:", err)
except ValueError as err:
print("ValueError:", err)
else:
print(r)
## おまけ：プログラムの実行速度を測ってみよう timeit
モジュールを使って、関数の実行速度を調べて見ます。
import timeit
timeit.timeit("fib(1)",setup="from __main__ import fib", number=100)/100
timeit.timeit("fib(10)",setup="from __main__ import fib", number=100)/100
timeit.timeit("fib(20)",setup="from __main__ import fib", number=10)/10
timeit.timeit("fib(30)",setup="from __main__ import fib", number=10)/10
timeit.timeit("fib(33)",setup="from __main__ import fib", number=1)
timeit.timeit("fib(36)",setup="from __main__ import fib", number=1)
timeit.timeit("fib(40)", setup="from __main__ import fib", number=1)
pyplot.semilogy()
pyplot.plot(
[1,5,10,15,20,22,25,30,32],
[timeit.timeit("fib(1)", setup="from __main__ import fib", number=100)/100,
timeit.timeit("fib(5)", setup="from __main__ import fib", number=100)/100,
timeit.timeit("fib(10)", setup="from __main__ import fib", number=100)/100,
timeit.timeit("fib(15)", setup="from __main__ import fib", number=10)/10,
timeit.timeit("fib(20)", setup="from __main__ import fib", number=10)/10,
timeit.timeit("fib(22)", setup="from __main__ import fib", number=10)/10,
timeit.timeit("fib(25)", setup="from __main__ import fib", number=1)/1,
timeit.timeit("fib(30)", setup="from __main__ import fib", number=1)/1,
timeit.timeit("fib(32)", setup="from __main__ import fib", number=1)/1,
]
)
tl=[1,5,10,15,20,22,25]
pyplot.semilogy()
pyplot.plot(
tl,
[timeit.timeit("fib({})".format(t), setup="from __main__ import fib",
number=5)/5
for t in tl])
pyplot.plot(
tl,
[timeit.timeit(f"fib({t})", setup="from __main__ import fib",
number=5)/5
for t in tl])
7. おまけその2：高速化に挑戦して見ましょう。¶
import logging
logging.getLogger('root').setLevel(logging.WARN)
#logging.getLogger('root').setLevel(logging.DEBUG)
def fib(n:int)->int:
logging.debug("-> fib({})".format(n))
if n == 0 or n == 1:
value= 1
else:
value= fib(n-1) + fib(n-2)
logging.debug(f"fib({n}) -> {value}")
return value
fib(4)
def fibb(n, buf={}):
logging.debug("-> fibb({},{})".format(n,buf))
if n not in buf:
if n == 0 or n == 1:
buf[n]=1
else:
buf[n]=fibb(n-2,buf)+fibb(n-1,buf)
logging.debug(f"fibb({n},{buf})->{buf[n]}")
return buf[n]
fibb(4,{})
fibb(10,{})
fibb(10)
d={}
fibb(10,d)
fibb(10,d)
def fibb(n, /, buf={}):
if n not in buf:
if n == 0 or n == 1:
buf[n]=1
else:
buf[n]=fibb(n-2,buf)+fibb(n-1,buf)
return buf[n]
[fibb(n) for n in range(11)]
pyplot.plot([fibb(n) for n in range(100)])
import timeit
timeit.timeit(
"fib(100)",
setup="""
def fib(n, buf={}):
if n not in buf:
if n == 0 or n == 1:
buf[n]=1
else:
buf[n]=fib(n-2)+fib(n-1)
return buf[n]
""",number=100)
timeit.timeit(
"""
fib(30)
""",
setup=
"""
def fib(n,buf=dict()):
if n == 0 or n == 1:
return 1
else:
return fib(n-1)+fib(n-2)
return buf[n]
""",
number=1)
m=0
d=m
def fib(n):
m=n
d=2*m
def fib1(n,buf={}):
nonlocal m
global d
d -=1
logging.debug(f"{m} {d} {n} {buf}")
if n not in buf:
if n in (0,1):
buf[n]=1
else:
buf[n]=fib1(n-2)+fib1(n-1)
logging.debug(f"{m} {d} {n} {buf} -> {buf[n]}")
return buf[n]
return fib1(n)
fib(10)
fib(11)
timeit.timeit("fib(1000)",setup="from __main__ import fib",number=10)/10
timeit.timeit("fib(1000)",globals=globals(),number=1)
def fib_b(n):
def fib1(n,buf={}):
print(n,buf)
if n not in buf:
if n in (0,1):
buf[n]=1
else:
buf[n]=fib1(n-2)+fib1(n-1)
print(n,buf,"->",buf[n])
return buf[n]
return fib1(n)
def fib_c(n):
buf={}
def fib1(n):
nonlocal buf # python version >= 3
print(n,buf)
if n not in buf:
if n in (0,1):
buf[n]=1
else:
buf[n]=fib1(n-2)+fib1(n-1)
print(n,buf,"->",buf[n])
return buf[n]
return fib1(n)
tl=[1,5,10,15,20,22,25]
pyplot.plot(
tl,
[timeit.timeit(f"fibb({t},dict())", setup="from __main__ import fibb",
number=5)/5
for t in tl])
pyplot.plot(
tl,
[timeit.timeit("fib({})".format(t), setup="from __main__ import fib",
number=5)/5
for t in tl])
8. Collatz 予想¶
数列の例としては、Collatz予想の数列も候補の一つです。
def collatz(n:int)->int:
"""
Collatz 予想：整数$n$から出発し、
nが偶数であれば2で割った値、さもなければ3*n+1を次の値とすることを
繰り返したとき、この数列は有限回で $1$に到達する。
"""
if n % 2 == 0:
return n//2
else:
return 3*n+1
n=14
while((n:=collatz(n))!=1):
print(n, end=", ")
# while文の例
# 「初めてのプログラミング」 7.3 ループの例題から
while (instr:=input("もう帰るの？"))!="さようなら":
print(instr)
print("またきてくださいね")
# version in Python.org
def fib_python(n):
a, b = 0, 1
while a < n:
a, b = b, a+b
return b
import timeit
timeit.timeit("fib_python(1000)", globals=globals(), number=1)