1. 数字の出現数を数える¶
1.1. プログラムの概要¶
あるシステムが生成する認証コードは6桁の整数です。このコードに現れる各桁の数字(Digit)の分布がどの程度一様なのかを調べます。
実際に生成されたコードの一覧から、各桁の数字に分解して頻度を数えます。
まずは生成されたcodeの一覧を変数codesに割り当てます。
#!python3
#-*- coding:utf-8 -*-
# '#'以降は行末までがコメントになります。(プログラムとしては実行されない)
nlen=6 # コードの桁数は6桁
codes=(
227524, 463251, 702567, 601620,
129458, 413239, 629380, 526093,
261547, 666552, 853626, 513298,
142167, 612906, 995697, 660500,
954404, 651454, 566439, 730975,
578967, 603424, 435636, 891667,
757294, 325567, 131075, 757309,
198547, 542718, 511525, 357679,
245280,
# 2021/05/14
40245, 314151, 689785, 246930, 429093,
546479, 240262, 631261, 559379, 869925,
814588, 766660, 588608, 815828, 946364,
542718, 710428, 725610, 863406, 250107,
629444, 865116, 86879,
# 012345 のように0から始まるcodeは, 0を省いて書くことにします。
)
次に一つの code の各桁に現れる数字の出現回数を数えます。 一番下の桁から順番にみていきます。
def count_digits(code,nlen=6): # 関数 `count_digits`を定義します。
# 最大二つの引数を持ちますが、二つ目の引数`nlen`は省略可能で、
# 省略された場合の値(既定値)は6です。
acc={} #これに数字毎の出現回数を入れていきます。
code=code+10**nlen # 最上位が0の場合を取り扱うために、10**nlenを足しておく。
# code =227524 であれば code=1227524とするということ。
while code>=10:
code, d=divmod(code, 10) #商 `code` と余り `d` に分解します。
# code=1227524 => code=122752,d=4
acc[d]=acc.get(d,0)+1
# accのkeyにdがあればその値に1を足したもの、さもなければ 0+1をacc[d]に設定する。
return acc
一覧表codesの全てのcodeに現れる数字に頻度を数えて、足していきます。
結果の度数分布表accを関数の値として返します。
def count_digits_in_list(codes,nlen):
acc={}
for code in codes: #codesの中に入っている全てのcodeについて
count=count_digits(code,nlen) #コードの中の数字の出現表を作る。
for d in count: #codeでの数字の出現数をaccに足して行く。
acc[d]=acc.get(d,0)+count[d]
return acc
codesの中の数字の度数分表を印刷し、ヒストグラムを表示させてみます。
import matplotlib.pyplot as pyplot #グラフ作成の準備のおまじない
import numpy
def main():
counts=count_digits_in_list(codes,nlen) #codeの一覧codesから数字の出現数の表を作成する。
print("digit: count")# 印刷する表のラベルを印刷する。
for d in sorted(counts): # 出現表にあらわれる数字を整列させた順番に、
print (d,":",counts[d]) # 数字(d)とその出現数(count[d])を印刷する。
# print("average:",len(codes)*nlen/10) #数字の出現数の平均値を印刷する。
print("average:", sum(counts.values())/len(counts)) # 6*len(codes)/10
print("std. dev:{:4.1f}".format(numpy.std(list(counts.values()))))
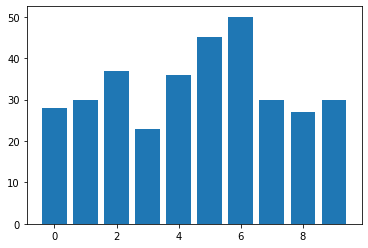
pyplot.bar(counts.keys(),counts.values()) # barグラフを印刷する。
pyplot.draw() #グラフ作成のおまじない
pyplot.show() #グラフ作成の最後のおまじない. Jupyter Notebookでは不要
#ファイルをコマンドとして実行するためのおまじない
if __name__ == "__main__":
main()
digit: count
0 : 28
1 : 30
2 : 37
3 : 23
4 : 36
5 : 45
6 : 50
7 : 30
8 : 27
9 : 30
average: 33.6
std. dev: 8.0
1.2. pandas/DataFrame¶
Data Analysis分野で最近よく使われるDataFrameオブジェクトを使うと、 短いプログラムでデータのリストから度数分表を取出し、またヒストグラムを表示させることができます。
import pandas # DataFrameが使えるようにpandasをインポートして置きます。
def split_digits(code,nlen=6):
acc=[] # あらわれた数字を順番に保存する。
code=code+10**nlen # 最上位が0の場合を取り扱うため
while code>=10:
code,d=divmod(code,10)
acc.insert(0,d)
return acc
def split_codes():
acc=[]
for code in codes:
acc +=split_digits(code)
return acc
# codesのデータを一桁の数字に分解し、リストをつくります
df=pandas.DataFrame(split_codes()).value_counts(sort=False)
print(df)
print("average:",numpy.average(df))
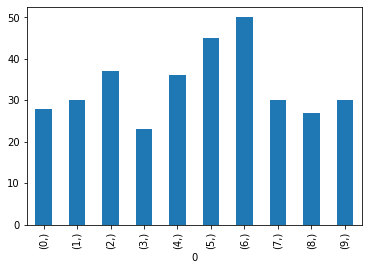
df.plot.bar()
0 28
1 30
2 37
3 23
4 36
5 45
6 50
7 30
8 27
9 30
dtype: int64
average: 33.6
<AxesSubplot:xlabel='0'>
1.3. matplotlib.pyplot¶
matplotlib.pyplotを使って、ヒストグラムの表示と度数分布を求めることも可能です。
まずヒストグラムを作成します。
counts, digits, chart = pyplot.hist(
split_codes(),
bins=range(0,11)
)
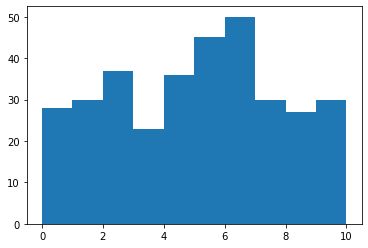
matplotlib.hist()関数は、ビン毎の計数値(count)、binの端の値(digits)そして、ヒストグラムのオブジェクトを値として返してきます。ですから、次のようなスクリプトで、各ビンのラベルと係数値を印刷します。digitsの要素数はcountsの要素数より1多いことに注意が必要です。
for p in (zip(digits,counts)):
print(p)
print("average:", sum(counts)/len(counts))
print(len(digits), ">",len(counts))
(0, 28.0)
(1, 30.0)
(2, 37.0)
(3, 23.0)
(4, 36.0)
(5, 45.0)
(6, 50.0)
(7, 30.0)
(8, 27.0)
(9, 30.0)
average: 33.6
11 > 10
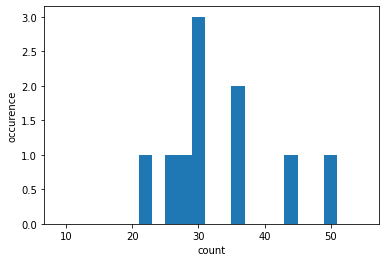
次に、数字の出現回数の分布をプロットしてみます。“5”および“6”の出現回数が突出していることが 見て取れます。
pyplot.hist(
counts,
histtype="stepfilled",
density=False,
align="left",
bins=range(34-3*8,34+3*8,2),
)
pyplot.gca().set_xlabel("count")
pyplot.gca().set_ylabel(u"occurence");
Text(0, 0.5, 'occurence')