30. 特殊相対論で考える２台の加速するロケットの運動

この章は琉球大学 前野昌弘さんのウェブページ「相対性理論をwebアプリで理解しよう」[A-1] の「２台のロケットのパラドックス」に触発されて作成されました。

上記のウェブページでは、移動する２台のロケット上の観測者と、 静止している観測者の3者の、それぞれの立場で見たときの他者の運動がわかりやすく説明されています。 上記のウェブページでは、２台のロケットは、時刻 \(t = 0\) にある速度で運動を始めますが、 加速は一瞬で終わる（加速中のロケットの位置は変わらないあるいは無視できるぐらい小さい）としています。

この加速中の運動を相対論的な運動方程式の解を使って確かめて見ようというのが、この章の目的です。

30.1. 加速しているロケットの軌道

今考えている問題では三人の登場人物（観測者）がいます。一人は、地上(慣性系)に静止しているの観測者です。残りの二人は、 この地上の観測者に対して一定の力を受けて加速運動を行っているそれぞれのロケットに乗っています [A-2] 。 2台のロケットは地上の観測者の座標系で見て、ロケットの進行方向に対して距離 \(L\) だけ隔てられているとします。

ロケット上の観測者の固有時間 \(\tau_i\;(i = 1,2)\) を使うと、慣性系でのロケットの軌道, \((Z_i(\tau_i), T_i(\tau_i)) i=1,2\), [ 図-30.1 の青実線:ロケット1、および　青の1点鎖線:ロケット2], は

(30.1)\[\begin{split}Z_i(\tau_i) \equiv & Z_i(0) + \frac{1}{\alpha}{\left\lbrace\cosh(\alpha \tau_i) -1\right\rbrace}\\ T_i(\tau_i) \equiv & \frac{1}{\alpha}\sinh(\alpha \tau_i)\end{split}\]

とかけます1。ここで、\(Z_i(0)\, (i=1,2)\) は2台のロケットの運動の初期状態(\(t=0\)でのそれぞれのロケットの位置)を表します。

また、パラメータ \(\alpha\) は,　相対論的な運動方程式：

(30.2)\[\begin{split}u_i(\tau_i) \equiv \frac{d Z_i}{d T_i} = \tanh (\alpha\tau) \\ \gamma_i(\tau_i) = \frac{1}{\sqrt{1 - u_i(\tau_i)^2}} = \cosh(\alpha\tau) \\ \frac{d}{d T_i} \left( \gamma_i u_i\right) = \frac{d\tau}{d T_i} \frac{d \sinh(\alpha\tau)}{d \tau} = \alpha \\\end{split}\]

から、相対論的な運動方程式での力(を静止質量 \(m_0\) で割ったもの）を表していると判ります。

次にそれぞれのロケットで固有時刻が \(\tau_i\) の時の瞬時静止系 \((x', t')\) を考えます。 つまり、その瞬間にロケットと同じ速度で慣性系に対して運動している系ということです 2 。 この瞬時静止系は地上の観測者に対して一定速度で運動していますから、慣性系とこの瞬時静止系はローレンツ変換で結ばれています。

(30.3)\[\begin{split}\begin{cases} x' = \gamma_\tau \left\lbrace (x - Z(\tau)) - u(\tau) (t - T(\tau)) \right\rbrace \\ t' = \tau + \gamma_\tau \left\lbrace (t - T(\tau)) - u(\tau) (x - Z(\tau)) \right\rbrace \\ \end{cases}\end{split}\]

慣性系（静止系）の座標系でみた2台のロケットの世界線と、 各時刻における瞬間静止系の座標系( \(x' = 0 \text{ and } t'= 0\) ) をグラフ( 図-30.1 ) および動画にして表示します。

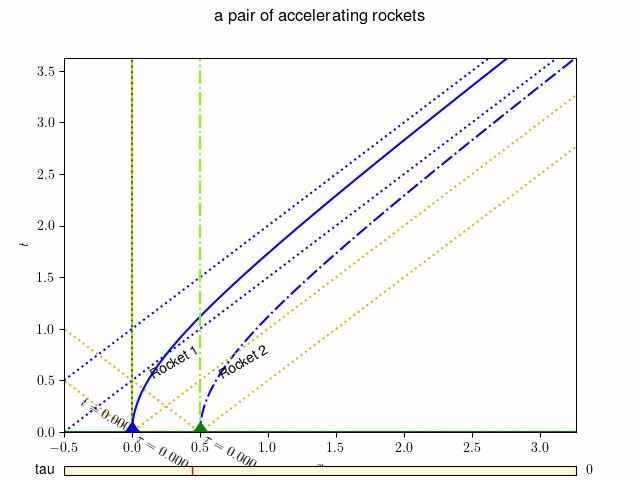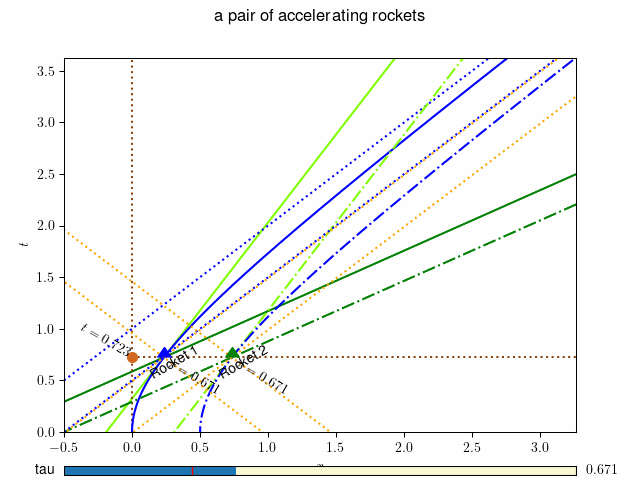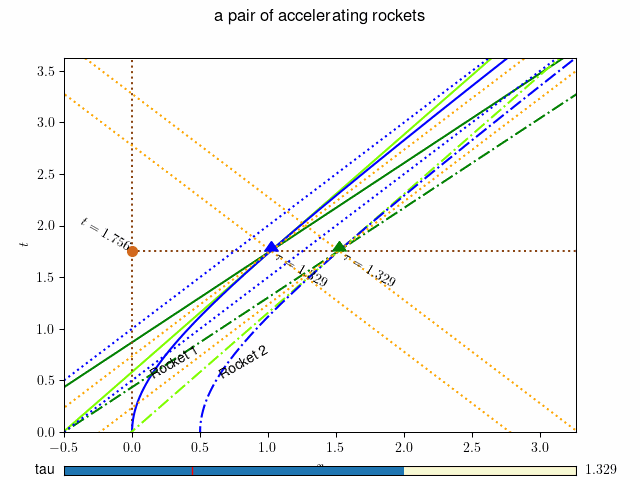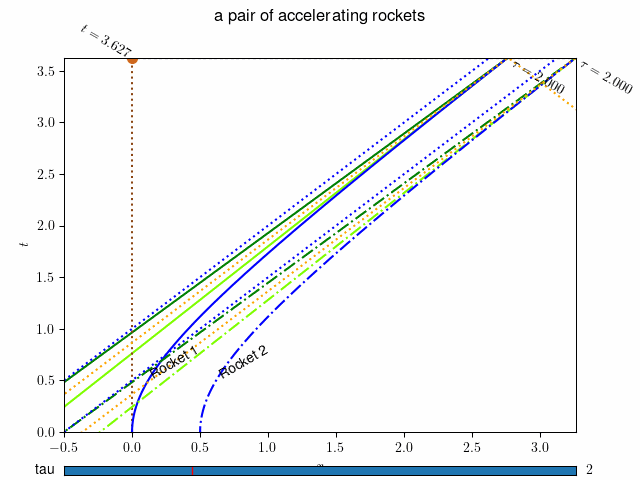
_images/ground.gif

図-30.2 地上の観測者によるロケットの世界線と座標系: 動画を表示するには ここをクリック(動画1) あるいはこちら http://www.j-parc.jp/ctrl/documents/articles/Relativity/_static/ground.mp4 。

グラフ 図-30.1 の横軸は慣性系の位置座標 \(x\) , 縦軸は時間軸 \(t\) となっています。なお、この図では \(c=1, \alpha=1\) としています。また、2台のロケットは出発時に距離 \(L = 0.5\) 離れていたとしています。 2台のロケットの世界線がそれぞれ青の実線(ロケット1）と一点鎖線（ロケット2）で示されています。 時刻 \(t=0\) では慣性系の \(x=0\) および \(x=0.5\) に静止していたロケットが、 徐々に速度を増して、光速度に近づいて行く様子がわかります。 この図(および動画）ではロケットの位置でのそれぞれの瞬間静止系の座標軸が緑色(時間軸)と濃緑色(空間軸)の実線(ロケット1) および 一点鎖線(ロケット2)で示されています。 ロケットの速度が増すに連れて、瞬時静止系の座標軸の傾きが変わって行きます。 これらの座標系の原点に示された数字(\(\tau=0.500\) など)はその時空点でのロケットの固有時刻 \(\tau\) を示しています。 オレンジの点線はロケットから発射された光がたどる世界線(の一部）です。青の点線は後で述べるように、ロケットの運動の漸近線をあらわしています。 慣性系の観測者は慣性系の同時刻(図では茶色の点線で示されています。)の2台のロケットの位置を時間とともに観測することになります。

次に時間の遅れについて考えてみます。 この図(図-30.1)の茶色の点線で示されている慣性系の同時刻線と比べることで、 静止系の観測者(SO)からは２台のロケットの時計(固有時刻)は同じように遅れて見えることがわかります。 数式で示せば、

(30.4)\[ \begin{align}\begin{aligned}\frac{d \tau}{d T} = \frac{1}{\frac{d T}{d\tau}} = \frac{1}{\cosh(\alpha \tau)} \le 1\\\tau = \int_0^{\tau} d\tau = \int_0^{T} \sqrt{1- v^2} dT \le \int_0^{T} dT = T\end{aligned}\end{align} \]

ということになります。

一方、加速が進んだ状態では、ロケット1のある時刻のロケット1の観測者(R1)はロケット２の時計は"進んでいる”と”観測”します。 逆に、進行方向の前方のロケット(Rocket 2) の観測者(R2)は後方のロケット(Rocket1)の時計は、遅れていると"観測"します。

この図からはまた、静止系でみた２台のロケットの距離が加速中も変わらないこともわかります。

一方、固有時刻が \(\tau_1\) の ロケット1の観測者が観測するロケット２の位置は、ロケット１の瞬時静止座標系でみて

(30.5)\[\begin{split}x'_2 =& L \cosh\left(\alpha\tau_{1}\right) + \left(\sqrt{L^{2} \sinh\left(\alpha\tau_{1}\right)^{2} + 1/\alpha^2} - 1/\alpha\right) \\ \gamma(\tau_1) =& \cosh(\alpha\tau_1)\end{split}\]

となります。 \(x'_2\) はロケット1からみたロケット2までのの距離となりますが、 静止系でみた距離 \(L\) よりも大きいことがわかります。

静止系では２台のロケットは 同時刻に速度０から一定の力を受けて同じ様に加速して行きます。 一方、ロケット１から見ると、ロケット２は加速され、ロケット1から遠ざかって行くように見えるということになります 3 。

30.2. ロケットの観測者からみた運動

式-30.1 からわかるように、ロケットの世界線は 式-30.6 の双曲線となります。

(30.6)\[\left((Z_i(\tau) - Z_i(0))+\frac{1}{\alpha}\right)^2 - T_i(\tau)^2 = \frac{1}{\alpha^2}\]

図-30.1 にこれらの双曲線の漸近線を青の点線で示しています。この漸近線より左の領域からでた光は、 ロケットが加速を続けている限り、ロケットには到達できないことに注意して置きます。 この現象を理解するために、静止系での時空間座標が \(t=0, x= L- \frac{1}{\alpha}\) である点4を、 ロケット2の固有時間 \(\tau\) 瞬間座標系で観測した場合の時刻を調べてみます 5 。

(30.7)\[\begin{split}\alpha t' =& \gamma\left( (t-T_2(\tau)) - v (x-Z_2(\tau))\right) \\ =& \gamma\left( -\sinh(\alpha\tau) + \tanh(\alpha\tau)\cosh(\alpha\tau) \right) \equiv 0\end{split}\]

となって、この時空点をロケット2の瞬間静止座標系でみたときの時刻は時刻 \(\tau\) に拘らず常に0 となります。 つまりロケット２から見るとこの時空点の時計は完全に止まっているようにみえることになります。 何れにせよ、ロケット2の加速が続く限り、世界線の漸近線より上の領域にある時空点からの情報は決してロケット2に届くことは無いので、 此の事をロケット2上の観測者が知ることは無いのですが6。

30.2.1. ロケットの観測者に固定された座標系

瞬間静止座標系では、ある時刻でロケットは静止して見えます。 しかし、ロケットは加速運動を続けているので、 次の瞬間にはこの座標系ではロケットはある速度を持って運動していることになります。 つまり、この座標系は、ロケットが静止して見える座標系（ロケットの空間座標が常に同じ）ではありません。 あるロケットが静止して見える座標系(\((\xi, \tau)\))を次の様に定義してみます。

まず時間座標は、そのロケットの固有時刻 \(\tau_i\) をとることにします。 静止系の座標が(\(x,t\))である時空点(\(P\))があったとき、 ロケットの時刻\(\tau\)での瞬時静止座標系での座標(\(x', t'\))は、

(30.8)\[\begin{split}x' =& \gamma_r(\tau) \left( x - Z_r(\tau) - U_r(\tau) \left( t - t_r(\tau)\right)\right) \\ t' =& \tau + \gamma_r(\tau) \left( - U_r(\tau) \left( x - Z_r(\tau) \right) + t - t_r(\tau)\right)\end{split}\]

となります。　この時空点のロケットの静止座標系(\(\xi, \tau\))での座標値を、

(30.9)\[\begin{split}\xi =& \gamma_r(\tau) \left( x - Z_r(\tau) - U_r(\tau) \left( t - t_r(\tau)\right)\right) \\ \tau =& \tau\end{split}\]

と定義します。明らかに、この座標系ではロケットは常に \(\xi=0\) の位置にあり、時間座標 \(\tau\)はロケットの固有時間そのものになっています。

このとき 任意の時空点に対するこの座標系での　\(\tau\) は慣性系の座標値(\(x, t\))から関係式,

(30.10)\[0 = \gamma_r(\tau) \left( - U_r(\tau) \left( x - Z_r(\tau) \right) + t - t_r(\tau)\right)\]

を満たす \(\tau\) として定義されます。 またこのとき、\(\xi\) は

(30.11)\[\xi =\frac{1}{\gamma_r(\tau)}\left(x-Z_r(\tau)\right)\]

です。

\(Zr(\tau)\) および　\(t_r(\tau)\) の具体的な表式を使って、整理すると、

(30.12)\[\tau = \frac{1}{\alpha} \tanh^{-1}\left(\frac{\alpha t}{1+ \alpha (x-L) }\right)\]

であることがわかります。これを、式-30.9 に代入することで、慣性系の座標からロケットの静止座標系への変換式として、

(30.13)\[\begin{split}\xi =& \frac{1}{\alpha\cosh(\alpha \tau)}\left[1+\alpha(x-L) - \cosh(\alpha\tau)\right] \\ \tau =& \frac{1}{\alpha} \tanh^{-1}\left(\frac{\alpha t}{1+ \alpha (x-L) }\right)\end{split}\]

が導かれました 7 。この式を逆に解くと、

(30.14)\[\begin{split}x =& L -\frac{1}{\alpha} + \frac{1}{\alpha}\left(1 + \alpha \xi \right) \cosh(\alpha\tau) \\ t =& \frac{1}{\alpha} \left(1 + \alpha \xi \right) \sinh(\alpha\tau)\end{split}\]

が導かれます 8 。

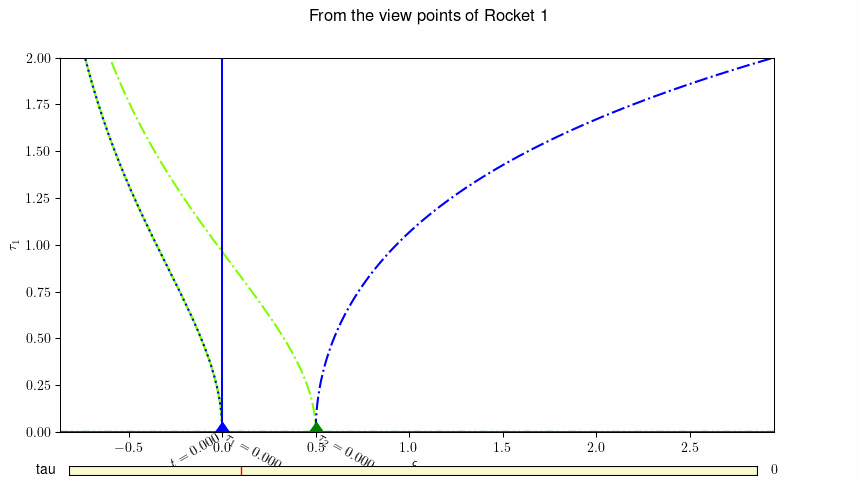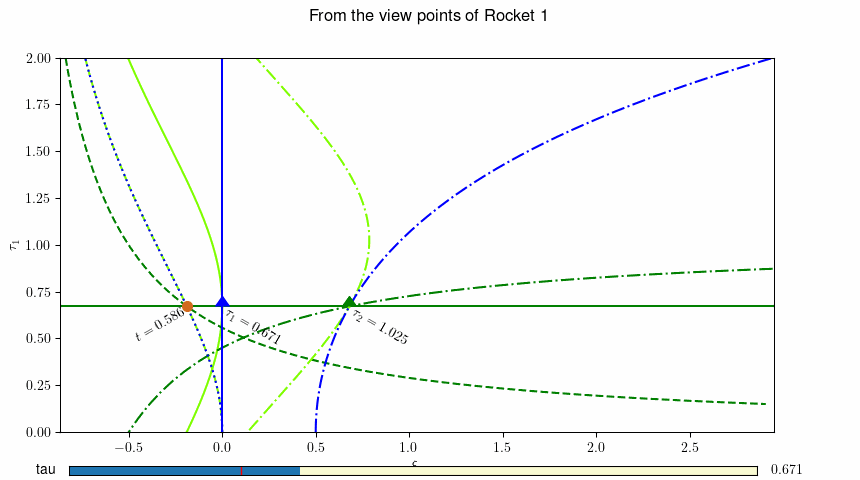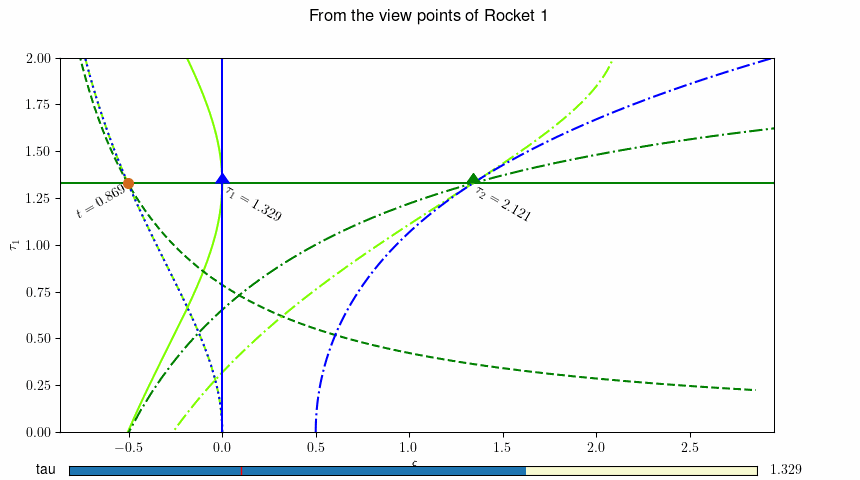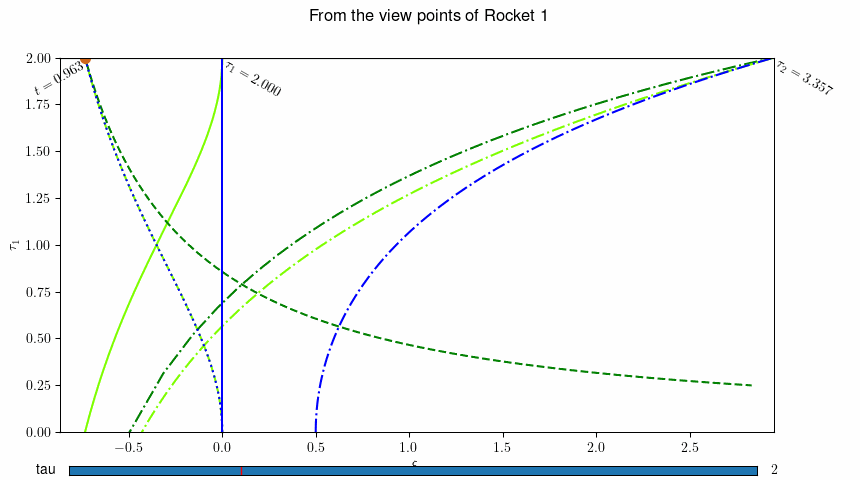
_images/rocket1.gif

図-30.4 ロケット１(青▲)の静止系から見た、地上の観測者(茶色●)とロケット２(緑▲)の運動。 動画を表示するには ここをクリック(動画2) あるいはこちら http://www.j-parc.jp/ctrl/documents/articles/Relativity/_static/rocket1.mp4 。 数字はそれぞれの観測者のその時空点での固有時を示しています。

このようにして導かれた Rocket-1(\(L=0\)) の静止座標系での、地上の観測者, Rocket-1 および Rocket-2 の軌跡を図示したものが、 図-30.3 です。 青の点線が地上の観測者、実線がRocket-1,　一点鎖線がRocket-2　の軌跡(世界線）を示しています． 緑色の線および濃緑色の線は、Rocket-1のある時刻 \(\tau\) でのそれぞれの観測者の瞬時静止座標系の時間軸(緑色）および空間軸(濃緑色）を 表しています。　地上の観測者の瞬時静止系の時間軸と世界線は、地上の観測者はその系に対して静止していることから、全く重なっており、区別がつきません。 瞬時慣性系の時間軸および空間軸は慣性系(地上の観測者に対して等速度で運動している座標系） でみれば直線となるべきですが、Rocket-1の静止座標系は慣性系では無いため、この図では曲線として表現されています。 ロケット2は急速に速度を上げて遠ざかって行きます。地上の観測者は、当初速度を上げながら遠ざかって行きますが、ある時点で減速に転じます。

脚注

1

なおこの章では光速度を 1 \(c = 1\) とした単位系を使うことにします。

2

このロケットの瞬時静止系で見れば、ロケットの座標は \(x'=0, t'=\tau\) となります。

3

ロケット２から見ると地上の観測者もロケット１も徐々に遠ざかって行くことになります。

4

図-30.1 では \(L=0.5, \alpha=1\) としましたので、この点は \(t=0, x=-0.5\) となります。

5

この点は、直前に述べたロケット２が一定の力学的力をうけたときの運動の漸近線上の点でもあります。

6

ロケットが加速を止めて、光速度以下の等速運動に入ればいずれこの情報を受け取ることができます。

7

この変換を用いると、無限小の四次元的な距離は、

(30.15)\[ds^2 = dt^2 - dx^2 =　\left(1+ \alpha \xi \right)^2 d\tau^2 - d\xi^2\]

と書けます。これから \(\tau\) は \(\xi=0\) の時空点の固有時と一致していることがわかります。

8

式-30.13の第２式から、 \(x<L-\frac{1}{\alpha}\) の領域では、実の \(\tau\) が存在すのは、 \(t\) が

(30.16)\[-\left(x - L + \frac{1}{\alpha}\right) < t < \left(x-L+\frac{1}{\alpha}\right)\]

の範囲にある時だけです。つまり、Rocket-1の静止座標系 \((\xi, \tau)\) は慣性系の空間 \((x,t)\) の全てをカバーすることはできません。