29. Rod and Hole パラドックス¶
「Rod and Hole (棒と穴)」パラドックスとは、棒の長さと同じ直径をもつ 穴があったとき、棒はこの穴を通過できるのだろうかという問題です。
穴の静止系で見れば、棒はローレンツ収縮により短くなっているので、 棒は穴を通過できそうです。一方棒の静止系から見れば、穴は進行方向に ローレンツ収縮を受けているのですから、棒は穴を通過できそうにありません。
ここでは、ローレンツ変換を使ってこの問題を検討してみましょう。
29.1. 問題の定式化¶
簡単のために、時空は1+1次元の空間を考えます。 棒はその静止系(chart \(X_R\) )での長さが \(L\) であるとします。また、棒の太さは無限小であるとします。穴は空間を2分する厚さ無限小の板に開いており、その直径を \(D\) とします。
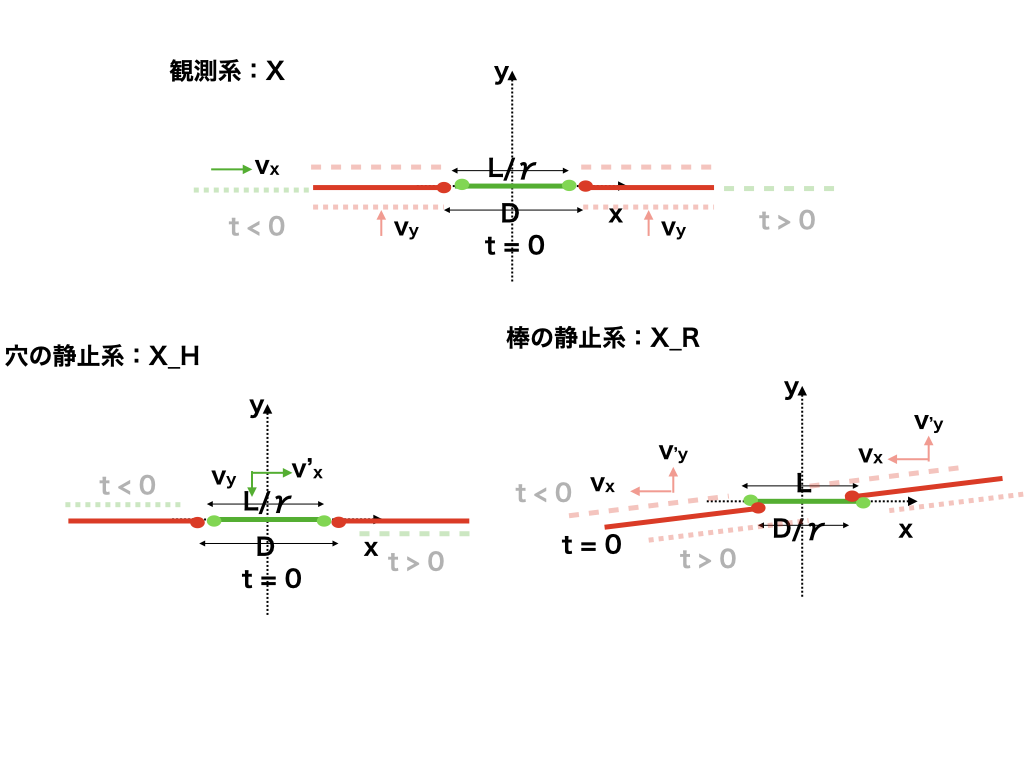
図-29.1 座標系ごとの棒と穴の動き¶
ここでは、長さ \(L\) の棒がその長手方向に速度 \(v\) で進行しており、 その長さとおなじ直径をもつ穴があるとしましょう。穴は棒の進行方向とは鉛直の方向に移動しており、穴と棒は時刻 \(t=0\) でその中心が一致するように 調整されているとします。
この穴が鉛直方向に移動し、棒が長さ方向に移動している系を、観測系 \(X_C\) と呼ぶことにします。
ローレンツ収縮によって、この系で観測する棒の長さは \(\sqrt{1-\beta^2} L\) となります。一方穴は直径方向には運動していませんので、 穴の直径は穴が静止しているときとなじ \(L\) です。したがって棒の長さは穴の直径より小さいので、棒は穴を通り抜けられるということになります。
一方、棒と一緒に運動している系( \(X_R\) )を考えると、この系では、穴は \(x\) 軸に逆方向に速さ \(v\) で動いていることになりますから、この系では、穴の進行方向の大きさは \(\sqrt{1-\beta^2} L\) です。 穴の大きさが棒の長さより短いので、棒は 穴を通らないではないかということになってしまいます。
また、穴が静止した座標系 \(X_H\) を考えることもできます。ここでは棒は穴に対して斜めに運動することになります。
以下ではローレンツ変換を使って、3つの観測系 \(X_C\), \(X_R\), \(X_H\) で棒と穴の運動がどのように見えるのかを調べることで、 この一見矛盾した状況が実は矛盾無く説明できることを明らかにしていきます。
29.2. 基準となる観測者 \(X_C\)¶
この座標系では、棒は水平方向に速度 \(v_x\) で進行し、穴は \(v_y\) で鉛直方向に動いています。 また、時刻 \(t=0\) で 穴の中心と棒の中心が(この座標系の原点で)一致するように、調整されてるとします。
棒の両端は棒の静止座標系ではその座標系の時間に関わらず、 その右端が \(x_r=L/2,y_r=0\),左端が \(x_l=-L/2,y_l=0\) の座標を持っています。
これをローレンツ変換を使って、観測系 \(X_C\) での座標を求めてみます。